逆向学习 0x0B 密码学进阶

加密的C实现

先学会怎么使用

MD5

使用

这里借用了一个MD5实现的cpp文件。

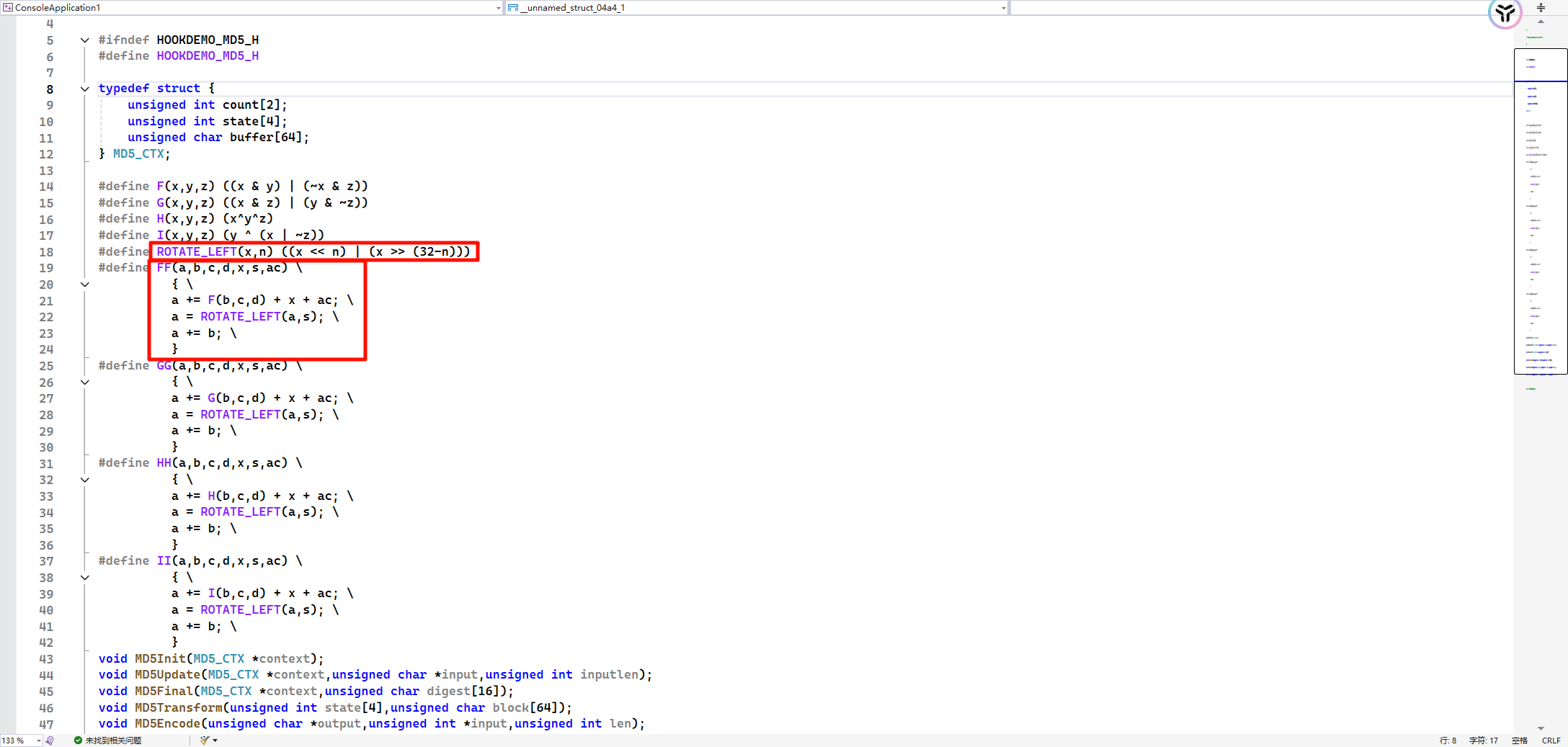
这个结构包括三个count：数据长度、state：算法初始化常量、buffer：明文数据

具体的先不管，用了再说

// 这里实现的MD5主要依靠一个结构体和三个方法
	// void MD5Init(MD5_CTX * context);
	// MD5Init方法需要一个MD5_CTX这个结构体的指针，就随便创建一个
	MD5_CTX content;
	MD5Init(&content);

	// void MD5Update(MD5_CTX * context, unsigned char* input, unsigned int inputlen);
	// MD5Updata方法需要传入结构体、明文数据、数据长度。两个都要是unsigned，无字符类型的
	const char* input = "a123456789";
	MD5Update(&content, (unsigned char*)input, strlen(input));
 
	// void MD5Final(MD5_CTX * context, unsigned char digest[16]);
	// 进行加密操作，传进去一个char来接收返回值
	unsigned char result[16];
	MD5Final(&content, result);

这样的得到的结果是 unsigned char 的形式，是不能直接查看的，需要进行一种编码，hex或者base64。

hex比较简单

   // 对加密结果进行hex编码
// 注意一定要是 3和33，防止溢出
   char temp[3] = { 0 };
   char finalResult[33] = { 0 };
   for (int i = 0; i < 16; i++)
   {
       int index = i;
       // 进行一个字符串的格式化输出，将结果的字节转换成16进制编码，取两位，不足补0
       sprintf_s(temp, sizeof(temp), "%.2X", result[index]);
       // 进行字符串拼接操作
       strcat_s(finalResult, sizeof(finalResult), temp);
   }
   cout << finalResult << endl;

这样就实现了一个MD5的简单使用

处理明文

MD5处理明文的过程

1、对明文进行hex编码

2、填充

将明文填充到448bit

先填充有关1，后面跟对应位数的0。 1000 0000

448/8 = 56，很显然不够正，因为还留了64bit，作为附加消息长度

附加长度之后是这样的：00 00 00 00 00 00 00 50 。

最后50计算是bit位，明文数据10字节，10*8bit = 80bit，转换成hex就是50

但是MD5是小端字节序应该变为： 50 00 00 00 00 00 00 00

明文最后处理成

61 31 32 33 34 35 36 37 38 39 ==80== …… 50 00 00 00 00 00 00 00

如果内容过长64bit放不下，就取低64bit。所有MD5输入长度可以无限大，SHA3算法同理

3、MD5输入数据无限大，不可能一起处理，需要分组

4、MD5的分组长度为512bit，数据需要处理到512的倍数，因此需要填充

5、填充位数为 1-512bit，如果明文长度刚好448bit，那么就填充512bit

字节序

所谓的字节序就是hex形式的字节在内存中的存放方式

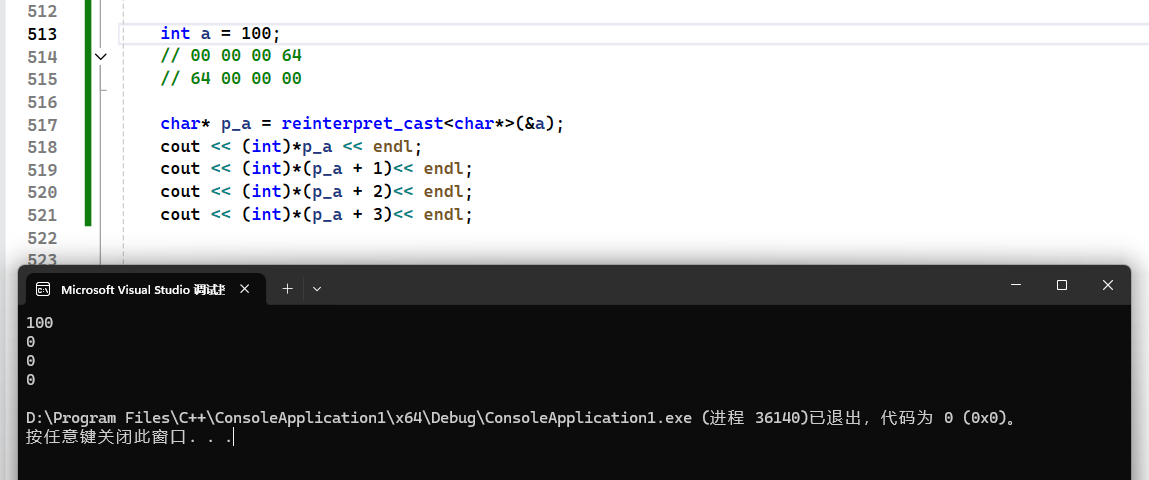
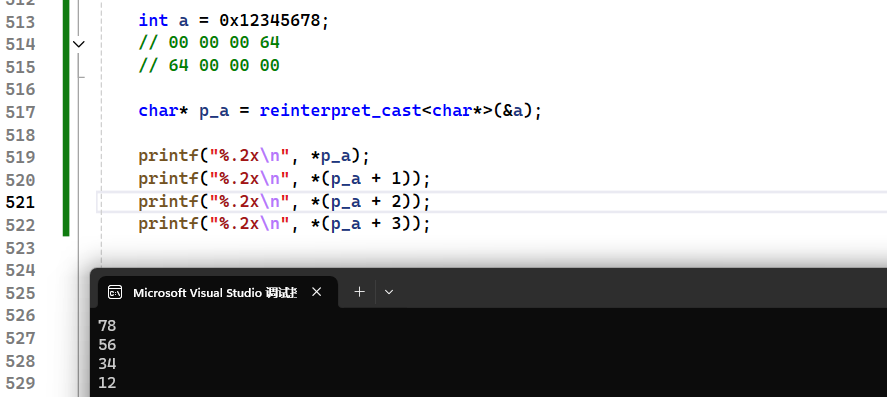
一个int类型占四个字节，定义一个100，按道理来说00 00 00 64，如果是这种存储方式那么就是大端字节序

通过定义 char，将字节挨个取出，发现在内存中是这样的 64 00 00 00，这就是小端字节序的存储，转换就是 1-4 2-3 3-2 4-1

也就是说如果内存中int数据为 78563412 的时候表示出来是0x12345678

算法细节

处理成512bit的明文数据之后，明文会分成16部分M1-M16，用于后续处理

1	61 31 32 33 34 35 36 37 38 39 80 00 …… 50 00 00 00 00 00 00 00

512/16 = 32bit，每组四字节

	实际需要的值	内存中小端字节序
M1	61 31 32 33	33 32 31 61
M2	34 35 36 37	37 36 35 34
M3	38 39 80 00	00 80 39 38
……	……	……
M15	50 00 00 00	00 00 00 50
M16	00 00 00 00	00 00 00 00

MD5的初始化常量

这个词在一开始创建结构体的时候提到过 state[4] 代表的是初始化常量，那么在MD5Init中干了什么呢

给初始化常量赋值

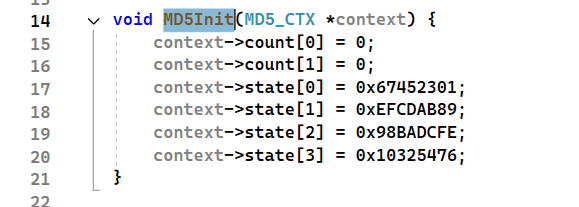
因为要求在内存中数据如下

A：01 23 45 67

B：89 ab cd ef

C：fe dc ba 98

D：76 54 32 10

所以在代码中按照以上方式进行赋值。给这玩意改了照样能算，能运行，但就是不是标准的MD5了

循环计算

这里的ABCD代表初始化常量，Mi就是上面的分组16组

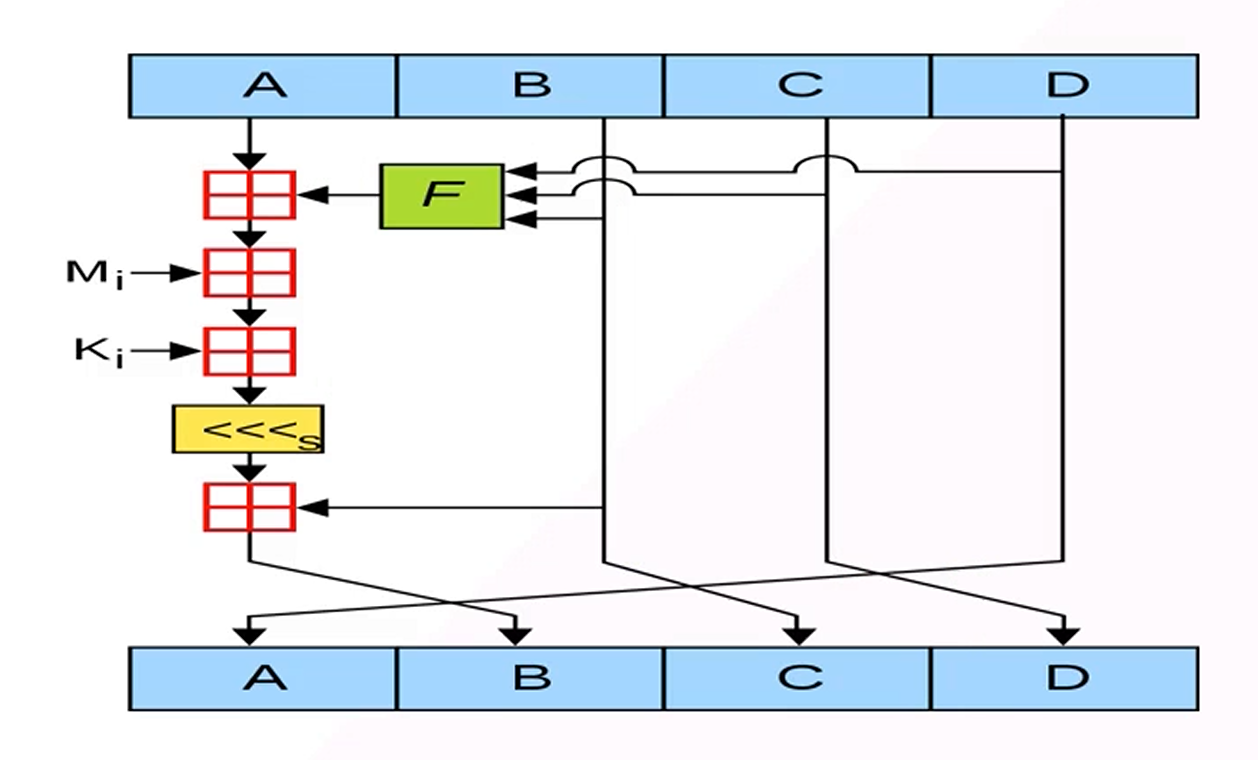
MD5总共64轮，每一轮会将旧的D直接给A，B-C，C-D，然后用旧的A来计算出新的B。

来看具体的操作，上图的 田 字就是表示加，Ki是数据常量是定值，看括号内最后一个参数就是K。K表中的值是由公式计算的，但是体现在代码中一般是常量，提高效率

s是循环左移的位数，这个也是常数，但是一般不会魔改这里，因为SHA0和SHA1的区别就是左移一位，SHA0则有安全性问题，左移我把握不住啊

F是函数，一共有四个函数，每个函数用16次 FF GG HH II

A + F(B, C, D) + Mi + Ki
<<<s
+ B

= new_B

也是一通操作，然后将64轮之后的ABCD拼接在一起，成为MD5值

代码实现

之前已经从理论上了解了算法的细节问题，尝试理解吸收，看看代码实现

先看这个结构体，count[2] 一共八个字节来表示数据长度，最多表示4G的数据

state[4] 初始化变量

buffer[64] 64*8 = 512 正好512bit，正好处理一轮数据的

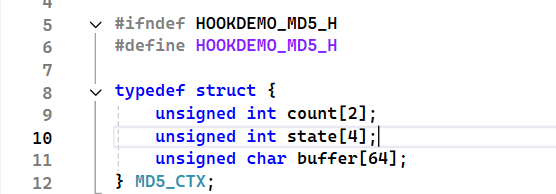
MD5Update方法是将传进来的数值进行计算，如果传入的数据不满64，也就是512bit，就暂存在Buffer中，如果数据长度到达了64，那么就开始计算这一组。因为可以多次Update，数据不够暂存是合理的

count两个值，一个计算的是明文长度，一个计算的是未使用的长度

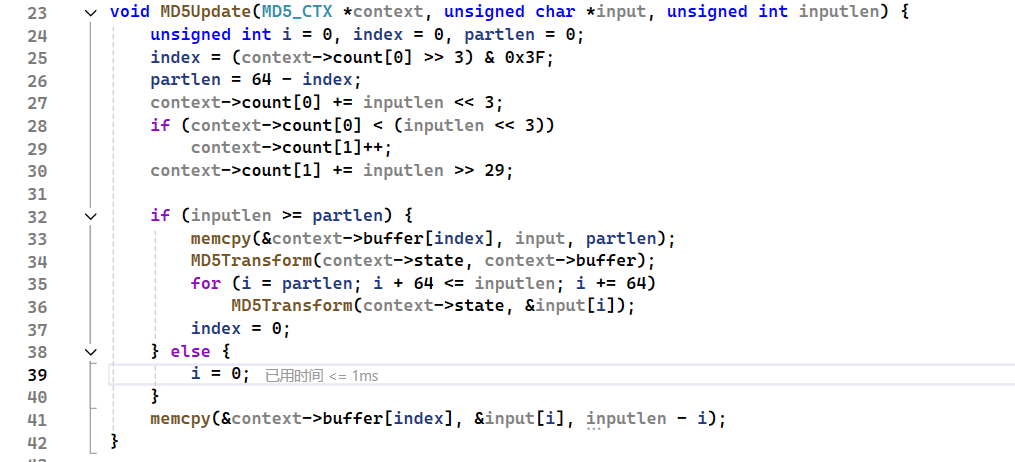
进入Final，先计算了长度，以及需要填充的长度，MD5Encode是完成了大端序到小端序的转换

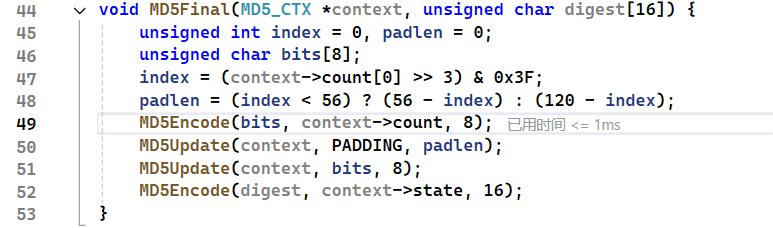
传进来int弄出去char*，就将int的四个字节拆开了，传进来的是count，只有两个int，bits是八个，就是用来计算末端的小端字节序的。

count的两个值为 72 0

虽然内存中分别为 72 00 00 00 、00 00 00 00。但是使用int来获取出来的还是大端字节序，使用异或和右移的方法，取出小端字节序来。和之前查看内存的小端字节序

以12 34 56 78为例。这是大端字节序，先异或将 78 作为output[0]，然后右移8位 00 12 34 56，再取出 56，再右移8位 00 00 12 34 ，取出 34 ，右移八位 00 00 00 12，取出12，最后的输出结果就是 78 56 34 12。

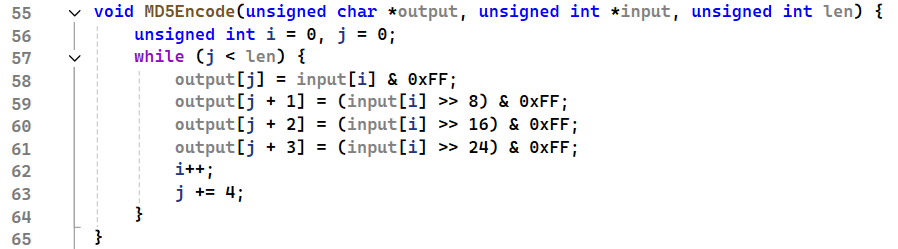
计算完之后，先压入padding，前面已经计算好了需要传入的个数，再压入字节序。压入bits的时候，就符合分组长度了，进入MD5Transform。

MD5Decode就是将64位的数据分成16组，M1-M16，主要通过左移来实现

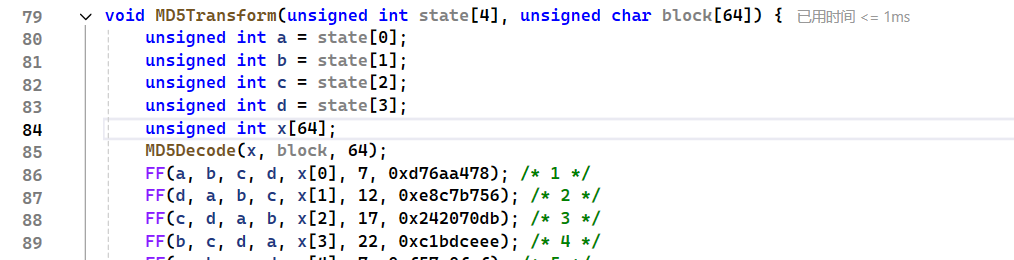
结尾处理实际+=，下一轮循环会继续拿着这个结果继续计算

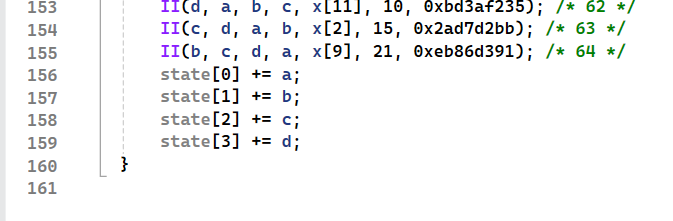
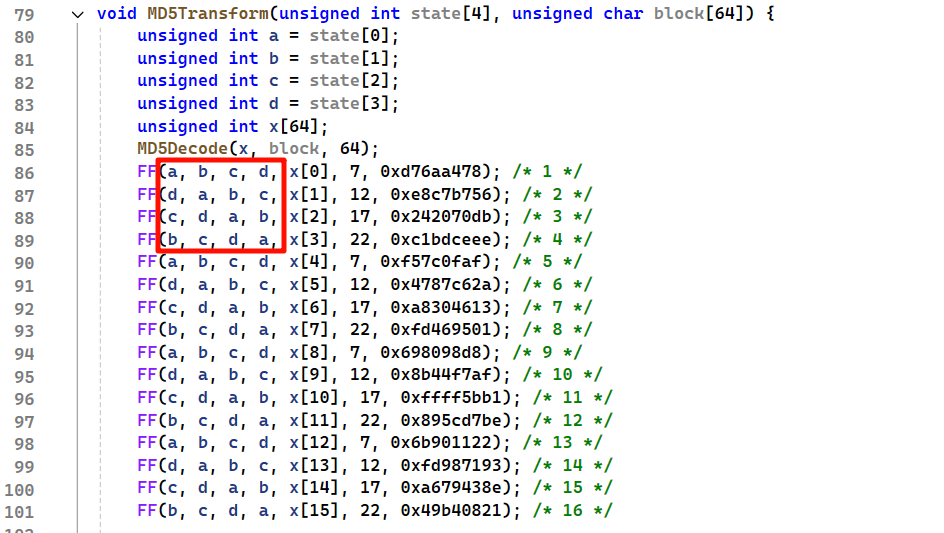
MD5Transform已经没啥好说的了，就是64次循环计算，利用四个函数来进行加的操作，然后每次循环产生新的B，最后得到一个新的 初始化常量 ，这个就是加密后的结果

计算完之后，得到初始化常量的数组，再次调用MD5Encode转换回来，得到MD5的计算结果

IDA插件

python环境

少年你是否还是一打开IDA先报个错呢。八成是python环境没弄好，启动 idapyswitch.exe 选中一个python环境即可，闪退不要紧，原地打开命令行，输入

1	idapyswitch.exe

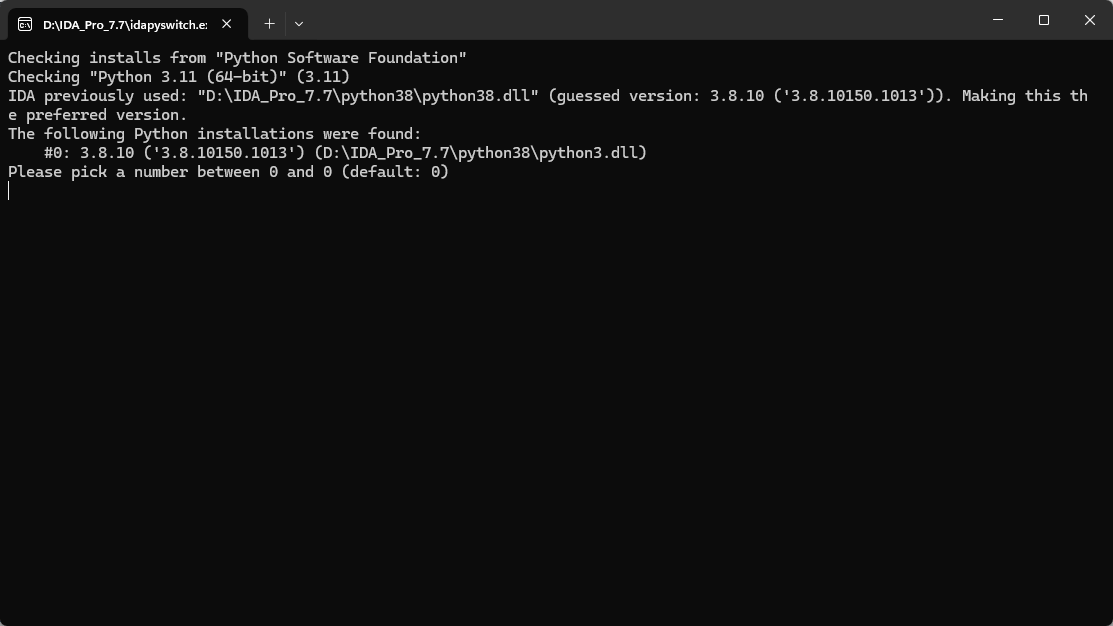
如果没有搜寻到电脑中的python版本也不要紧，我就没搜到，使用命令告诉他在哪

1	idapyswitch --force-path yourPath

成功之后，妈妈再也不用担心我打开IDA被叮咚吓一跳了

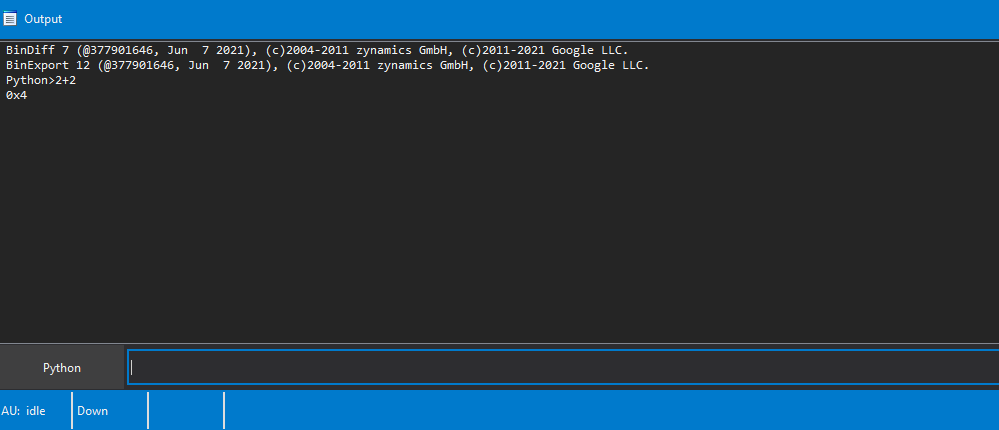
认识IDA

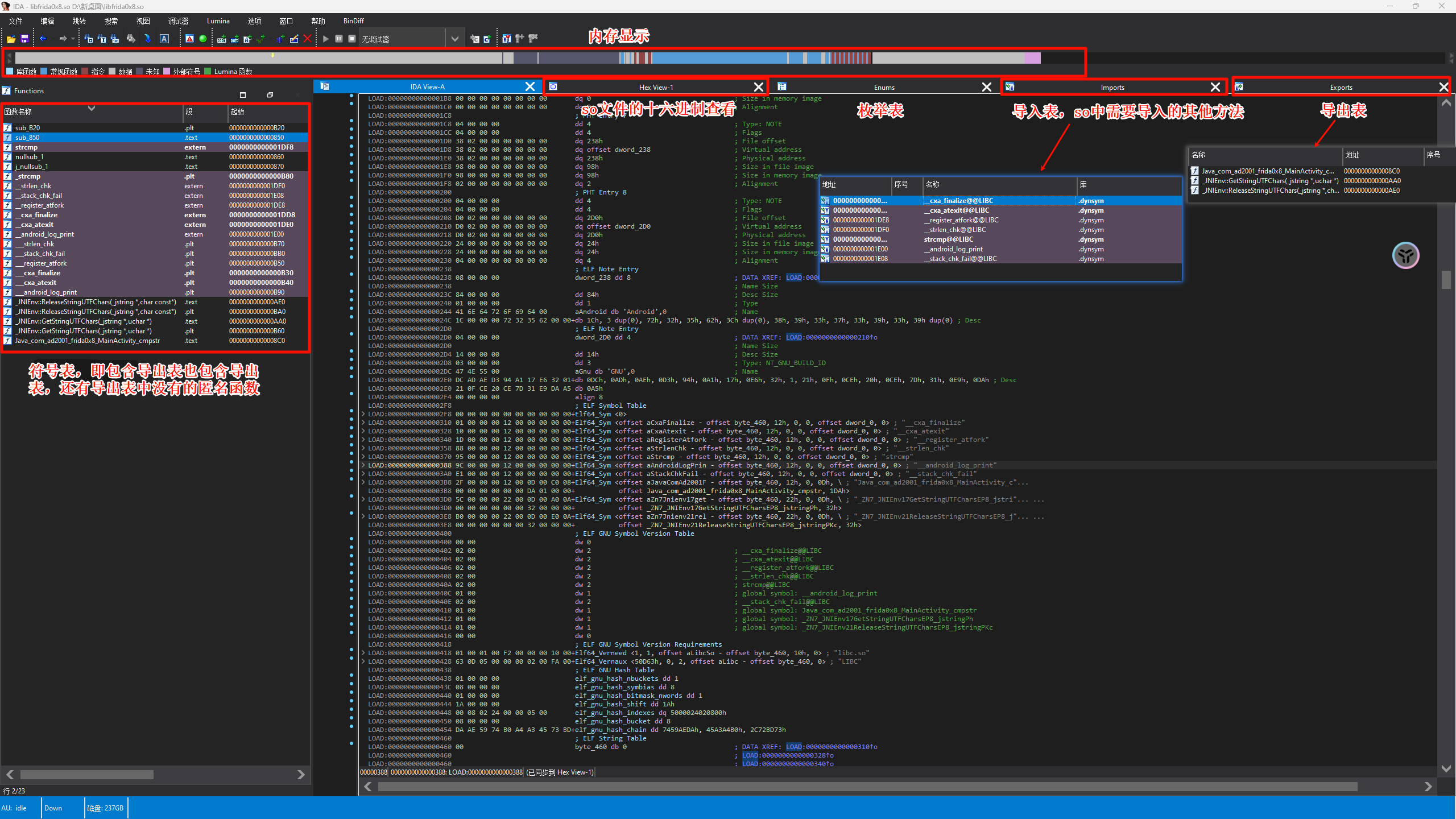
快捷键

CTRL+S 查看段信息，在IDA-View中，开头也是包含段信息的

段信息	含义
.text	表示代码段
.data	表示数据段，包含全局变量和静态变量
.bss	未初始化数据段
.rodata	只读数据段，如字符串常量
.rdata	资源数据段
.symtab	符号表，包含函数名和变量名
.strtab	字符串表
.rela	重定位段
.hash	哈希表
.dynsym	动态符号表
.dynstr	动态字符串表
.dynamic	动态链接信息
.plt	过程链接表
.got	全局偏移表

快捷键，无需多言

快捷键	作用
F5	反编译为伪C代码
ctrl+s	查看段
Tab	切换代码窗口和反编译窗口
空格	切换代码窗口和图形窗口
C	将数据转为代码
G	地址跳转
X	交叉引用
Shift+;	添加注释
ESC	返回上一步
Shift+F12	打开字符串窗口
F1	帮助
F2	添加断点
A	转换为ASCII码
D	转换定义数据
H	转换10进制和16进制
M	更改符号常量
N	更改变量的名称
P	将代码定义为函数
Y	更改变量的类型/函数类型
Shift+F3	打开函数列表
Shift+F5	打开签名列表
Shift+F9	打开结构体窗口

插件

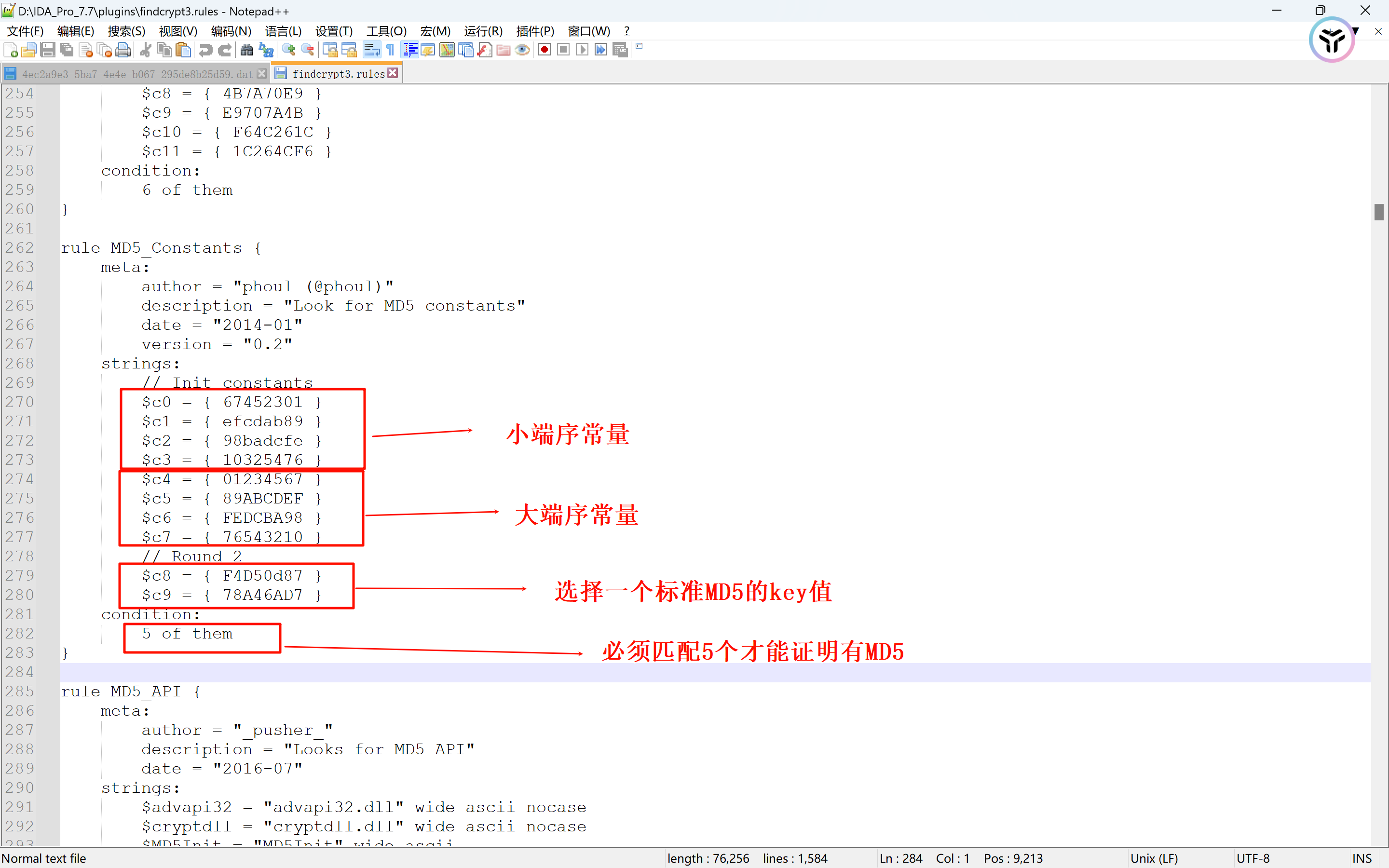
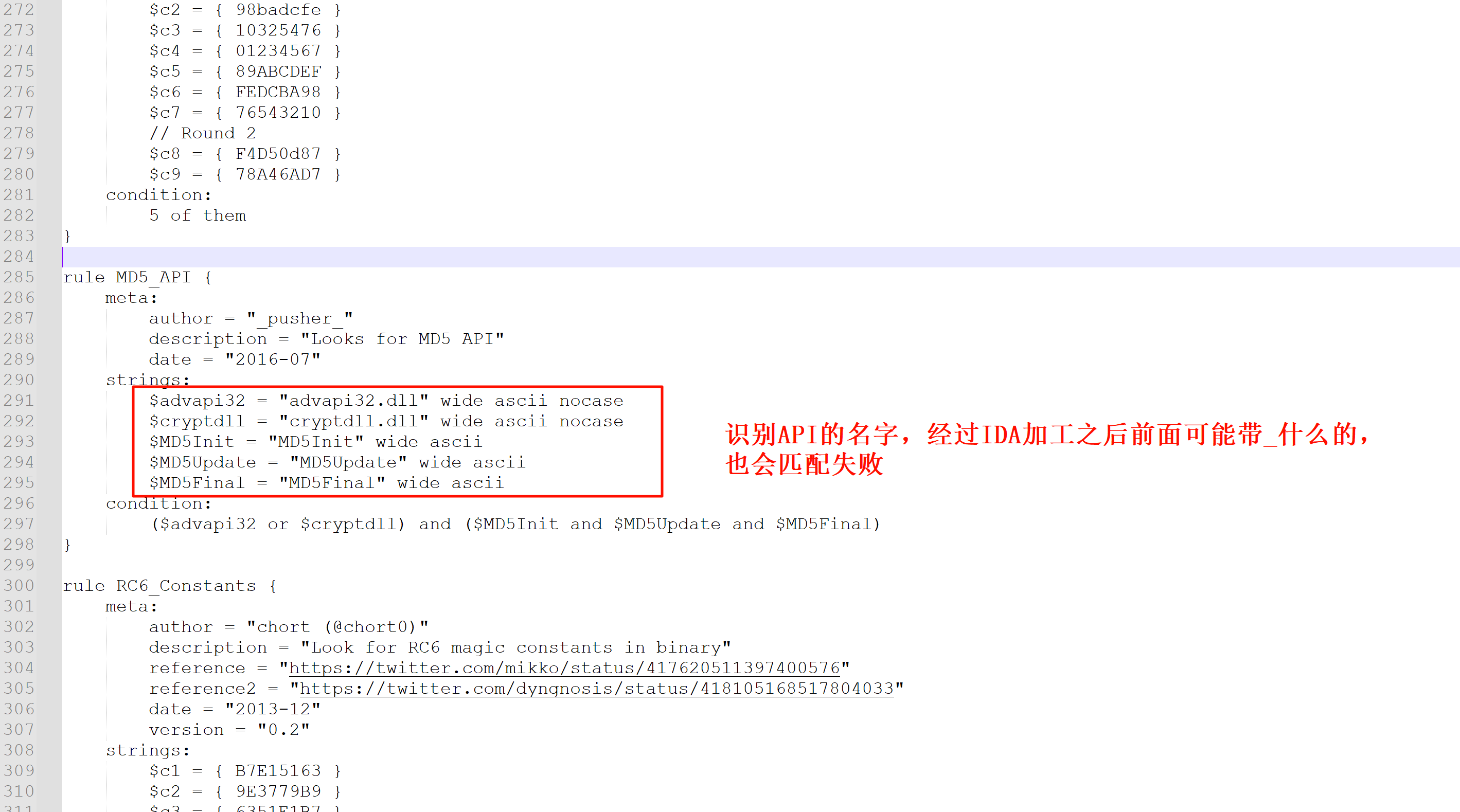
自带的F5插件不多说，和算法有关的还有几个插件 Findcrypt Signsrch

Findcrypt 主要是对于AES、DES算法的识别对哈希算法识别效果并不理想，但是也是可以识别出来一部分的

看一下他的匹配规则，有些时候有混淆什么的，太绝对了，匹配效果不是很好

利用findhash插件自吐

findhash插件可以检测哈希函数，并且生成一个frida代码，并且这个代码是可以进行hook打印地址信息的

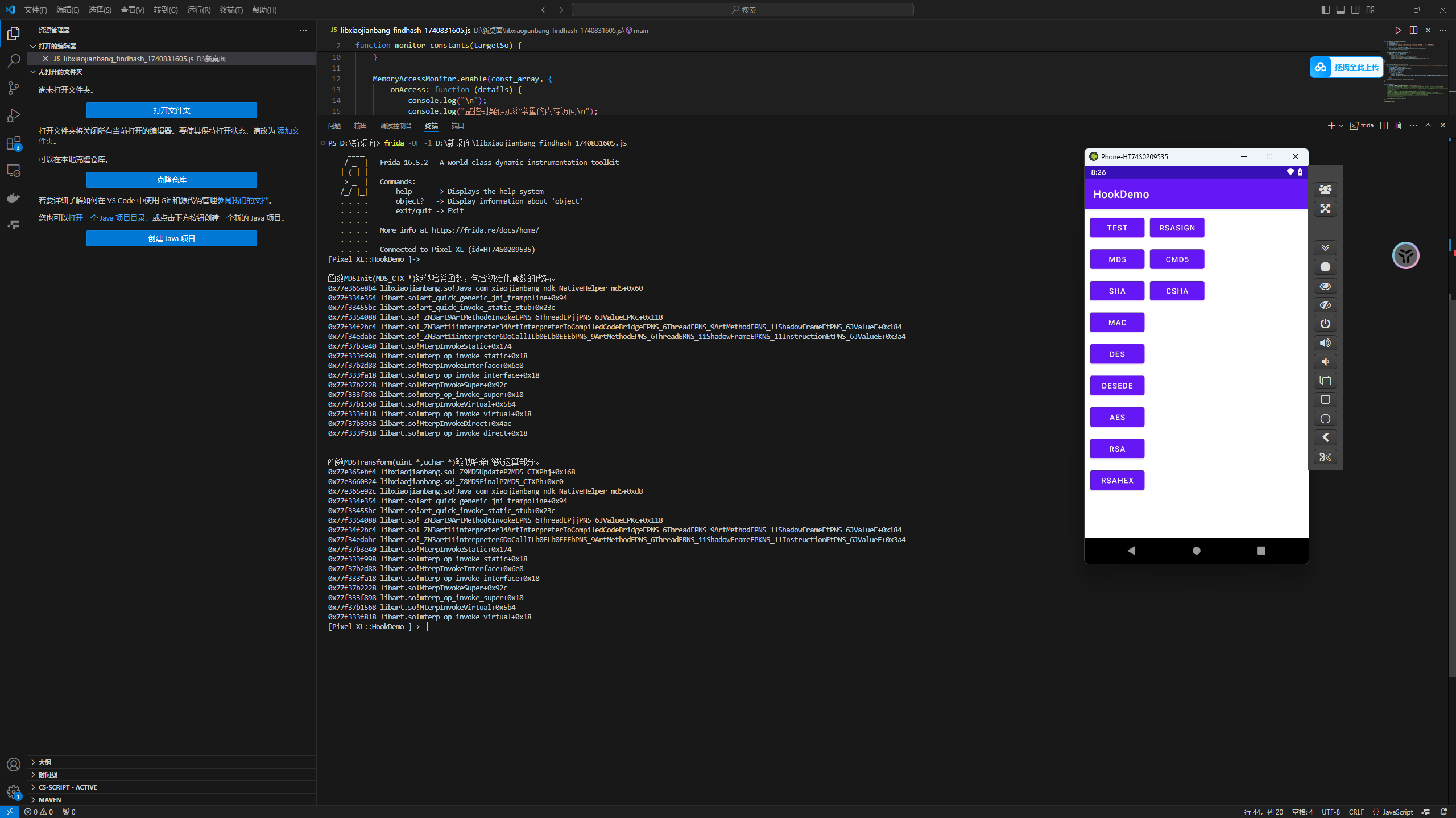
这样利用这个代码距离自吐算法还差打印一些参数，但是呢这个插件识别的方法有限。

在生成的js脚本中添加两个方法来打印传入值和返回值（C一般没返回值，打印运行结束后的传入值）

function print_arg(addr) {
    // 查找该地址所处模块，如果有模块，打印该模块的十六进制内容，如果为null（无模块）返回地址指针
    var module = Process.findRangeByAddress(addr);
    if (module != null) {
        return hexdump(addr) + "\n"
    } else {
        return ptr(addr) + "\n"
    }
}

function hook_native_addr(funcPtr) {
    // 查找该函数所处模块，钩取函数，下俩钩子，分别在函数执行前和函数执行后用于打印参数
    var module = Process.findModuleByAddress(funcPtr);
    Interceptor.attach(funcPtr, {
        onEnter: function(args) {
            this.args0 = args[0];
            this.args1 = args[1];
            this.args2 = args[2];
            this.args3 = args[3];
            this.logs = [];
            // 将模块名称和函数偏移地址（ptr(funcPtr).sub(module.base)）以及四个参数的内容记录
            this.logs.push("\n" + "call " + module.name + "!" + ptr(funcPtr).sub(module.base) + "\n");
            this.logs.push("this.args0 onEnter: " + "\n" + print_arg(this.args0));
            this.logs.push("this.args1 onEnter: " + "\n" + print_arg(this.args1));
            this.logs.push("this.args2 onEnter: " + "\n" + print_arg(this.args2));
            this.logs.push("this.args3 onEnter: " + "\n" + print_arg(this.args3));
        }, 
        onLeave: function(retval) {
            this.logs.push("this.args0 onLeave: " + "\n" + print_arg(this.args0));
            this.logs.push("this.args1 onLeave: " + "\n" + print_arg(this.args1));
            this.logs.push("this.args2 onLeave: " + "\n" + print_arg(this.args2));
            this.logs.push("this.args3 onLeave: " + "\n" + print_arg(this.args3));
            this.logs.push("return value: " + "\n" + print_arg(retval));
            console.log(this.logs.join("\n"));
        }
    })
}

traceNatives插件

这个插件是生成一个txt文件，文件内是frida指令，hook了他所检测到的一些函数偏移地址

直接运行看看

1	frida-trace -UF -O .\libxiaojianbang_1740836169.txt

这个是将函数调用的流程给打印了下来

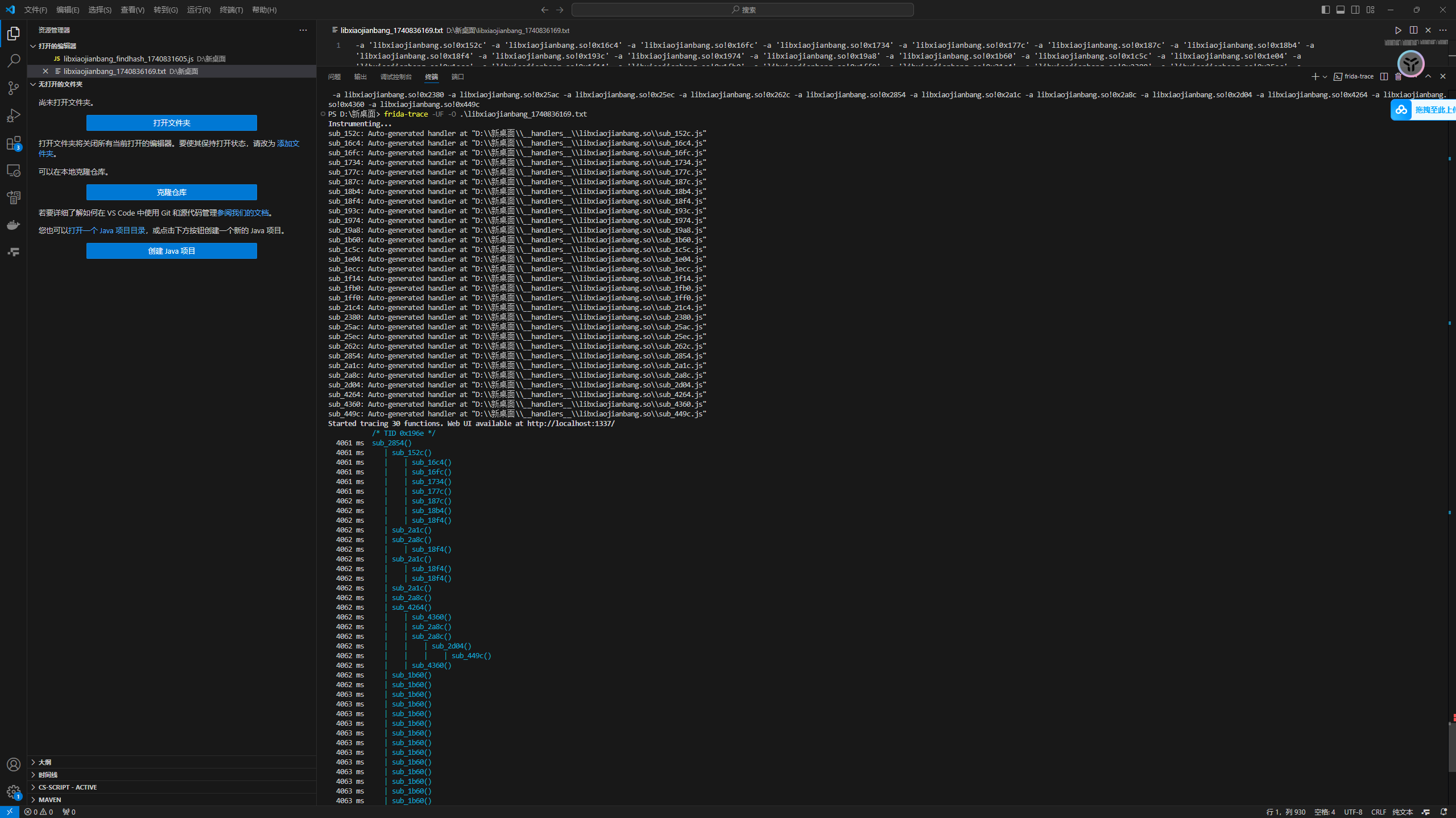
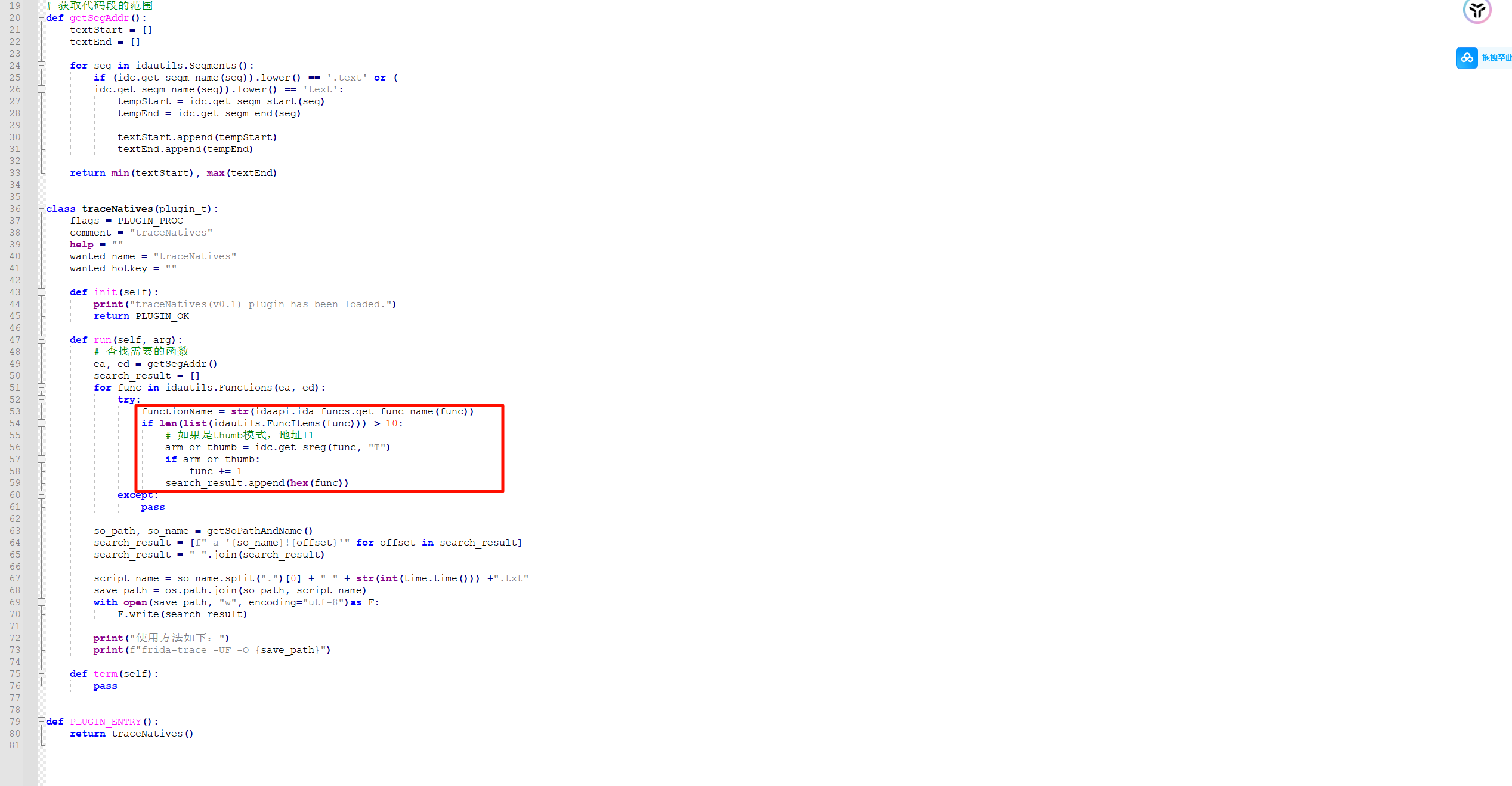
研究一下py文件

这个东西是将代码超过十行的方法记录下来，然后利用frida-trace将这些函数hook掉，打印函数调用流程

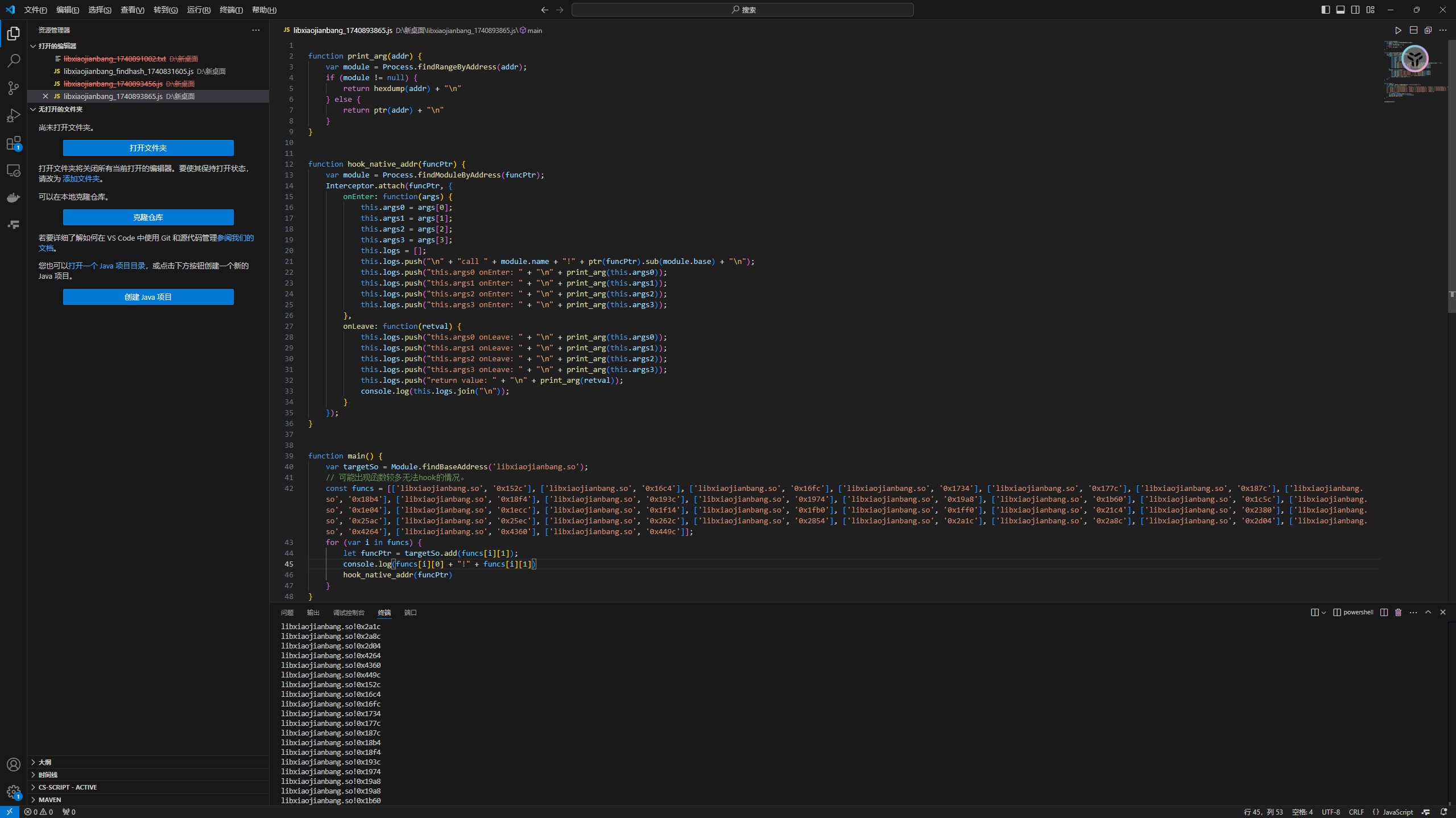
小改一下

def generate_script(funclist, so_name):
    script_module = """
function print_arg(addr) {
    var module = Process.findRangeByAddress(addr);
    if (module != null) {
        return hexdump(addr) + "\\n"
    } else {
        return ptr(addr) + "\\n"
    }
}
        

function hook_native_addr(funcPtr) {
    var module = Process.findModuleByAddress(funcPtr);
    Interceptor.attach(funcPtr, {
        onEnter: function(args) {
            this.args0 = args[0];
            this.args1 = args[1];
            this.args2 = args[2];
            this.args3 = args[3];
            this.logs = [];
            this.logs.push("\\n" + "call " + module.name + "!" + ptr(funcPtr).sub(module.base) + "\\n");
            this.logs.push("this.args0 onEnter: " + "\\n" + print_arg(this.args0));
            this.logs.push("this.args1 onEnter: " + "\\n" + print_arg(this.args1));
            this.logs.push("this.args2 onEnter: " + "\\n" + print_arg(this.args2));
            this.logs.push("this.args3 onEnter: " + "\\n" + print_arg(this.args3));
        }, 
        onLeave: function(retval) {
            this.logs.push("this.args0 onLeave: " + "\\n" + print_arg(this.args0));
            this.logs.push("this.args1 onLeave: " + "\\n" + print_arg(this.args1));
            this.logs.push("this.args2 onLeave: " + "\\n" + print_arg(this.args2));
            this.logs.push("this.args3 onLeave: " + "\\n" + print_arg(this.args3));
            this.logs.push("return value: " + "\\n" + print_arg(retval));
            console.log(this.logs.join("\\n"));
        }
    })
}


function main() {
    var targetSo = Module.findBaseAddress('$$$.so');
    // 可能出现函数较多无法hook的情况。
    const funcs = $$$funcs;
    for (var i in funcs) {
        let funcPtr = targetSo.add(funcs[i][1]);
        console.log(funcs[i][0] + "!" + funcs[i][1])
        hook_native_addr(funcPtr)
    }
}


setImmediate(main);
    """
    hookscript = script_module.replace("$$$funcs",str(funclist)).replace("$$$.so", so_name)
    return hookscript



class traceNatives(plugin_t):
    flags = PLUGIN_PROC
    comment = "traceNatives"
    help = ""
    wanted_name = "traceNatives"
    wanted_hotkey = ""

    def init(self):
        print("traceNatives(v0.1) plugin has been loaded.")
        return PLUGIN_OK
        


    def run(self, arg):
        # 查找需要的函数
        ea, ed = getSegAddr()
        search_result = []
        result_js = []
        so_path, so_name = getSoPathAndName()
        for func in idautils.Functions(ea, ed):
            try:
                functionName = str(idaapi.ida_funcs.get_func_name(func))
                if len(list(idautils.FuncItems(func))) > 10:
                    # 如果是thumb模式，地址+1
                    arm_or_thumb = idc.get_sreg(func, "T")
                    if arm_or_thumb:
                        func += 1
                    search_result.append(hex(func))
                    result_js.append([so_name, hex(func)])
            except:
                pass

        
        search_result = [f"-a '{so_name}!{offset}'" for offset in search_result]
        search_result = " ".join(search_result)

        # 生成txt
        script_name = so_name.split(".")[0] + "_" + str(int(time.time())) +".txt"
        save_path = os.path.join(so_path, script_name)
        with open(save_path, "w", encoding="utf-8")as F:
            F.write(search_result)
            
        
        # 生成js脚本
        myscript = generate_script(result_js, so_name)
        
        script_jsname = so_name.split(".")[0] + "_" + str(int(time.time())) + ".js"
        save_jspath = os.path.join(so_path, script_jsname)
        with open(save_jspath, "w", encoding="utf-8") as F:
            F.write(myscript)

        print("txt使用方法如下：")
        print(f"frida-trace -UF -O {save_path}")
        print("生成地址hook js脚本（自用）")
        print(f"frida -UF -l {save_jspath}")
        

    def term(self):
        pass

再生成一个js文件，将超过十行的函数hook一下

SHA1

初步认识

1、SHA1算法对于明文的处理和MD5相同，区别是最后的消息长度是==大端字节序==（SHA家族的都是大端字节序）。SHA1和MD5都是从MD4算法改进出来的算法，基本思路都是将信息分为N个分组，每组64字节（512bit），每个分组都进行摘要运算。当一个分组运算完毕之后，将上一个分组的结果用于下一个分组的运算（感觉很像CBC模式，但是CBC模式是保留中间过程的运算结果的，信息摘要只保留最后一次的运算结果）。明文信息长度（bit长度，而非字节长度）用64bit表示，是作为补充信息在最后一个分组的末尾

示例：
明文：abc
明文长度为：3*8=24，24用十六进制表示 18
大端字节序表示长度： 00 00 00 00 00 00 00 18                 4*16=64，最后64字节表示长度
小端字节序表示长度： 18 00 00 00 00 00 00 00
填充：
61 62 63 80 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 ……（最后64位根据MD5和SHA1算法的不同使用不同的字节序）

2、SHA1的分组长度是512bit，明文也要分段，类似Mi，区别是有80段（MD5有16个段M1-M16），SHA1的前16段也是对512字节进行分段，但是还扩展了64段，一共80段。遵循大端字节序，在代码中不需要像MD5一样看着很别扭

3、SHA1和SHA0的区别就是在扩展这64段的时候，增加了循环左移一位，仅一行的差别

1 2	W[t] = SHA1CircularShift(1, W[t-3]^W[t-8]^W[t-14]^W[t-16]); ——SHA1 W[t] = W[t-3]^W[t-8]^W[t-14]^W[t-16]; ——SHA0

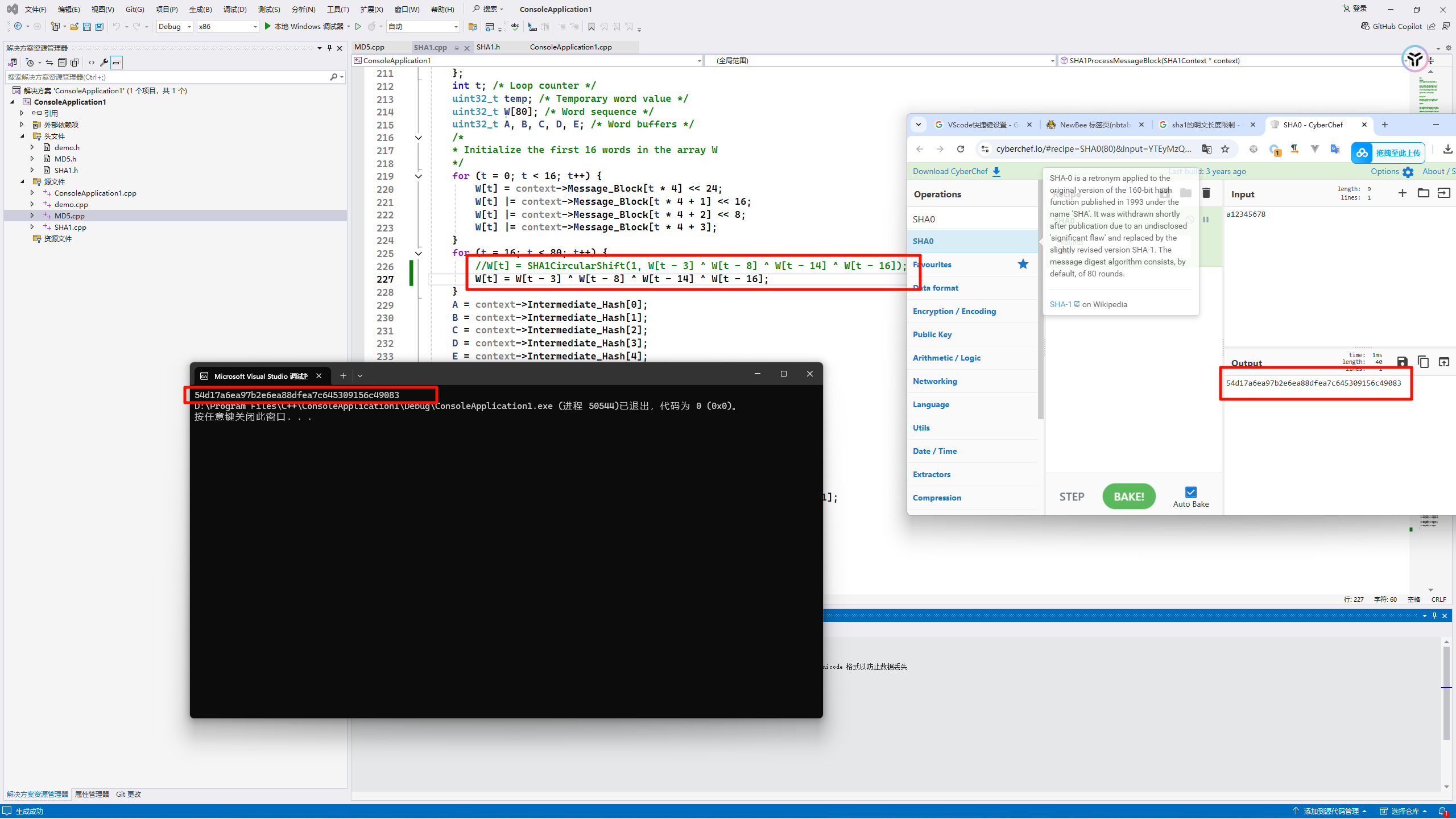
但是就是差这一位的左移，导致SHA0有安全隐患，因此在魔改算法的时候，一般不会对左右移下手

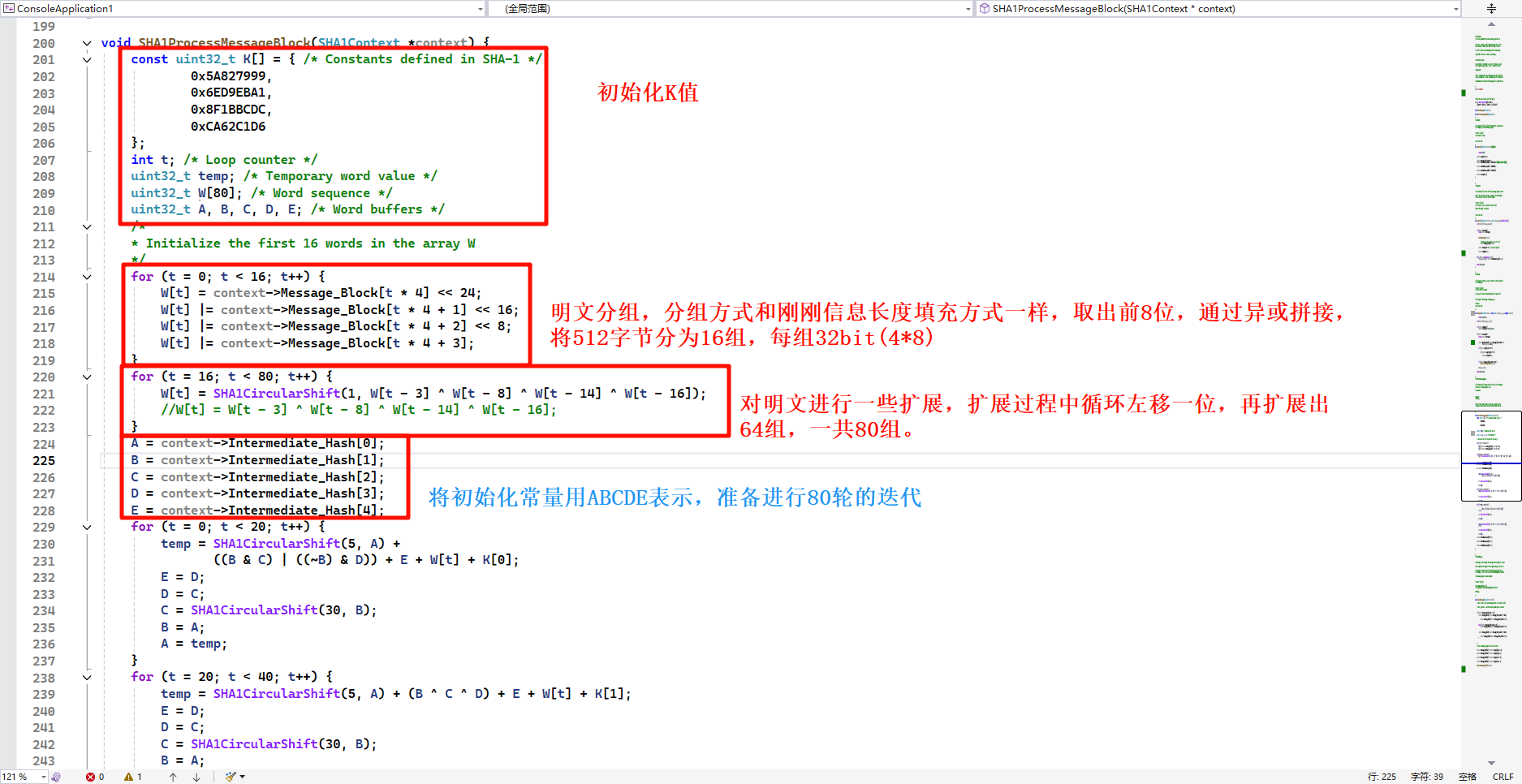
4、SHA1的核心计算过程和MD5差不多，区别是K值只有四个，每二十轮用一个，总共80轮。MD5的K值是有64个的，每轮用一个

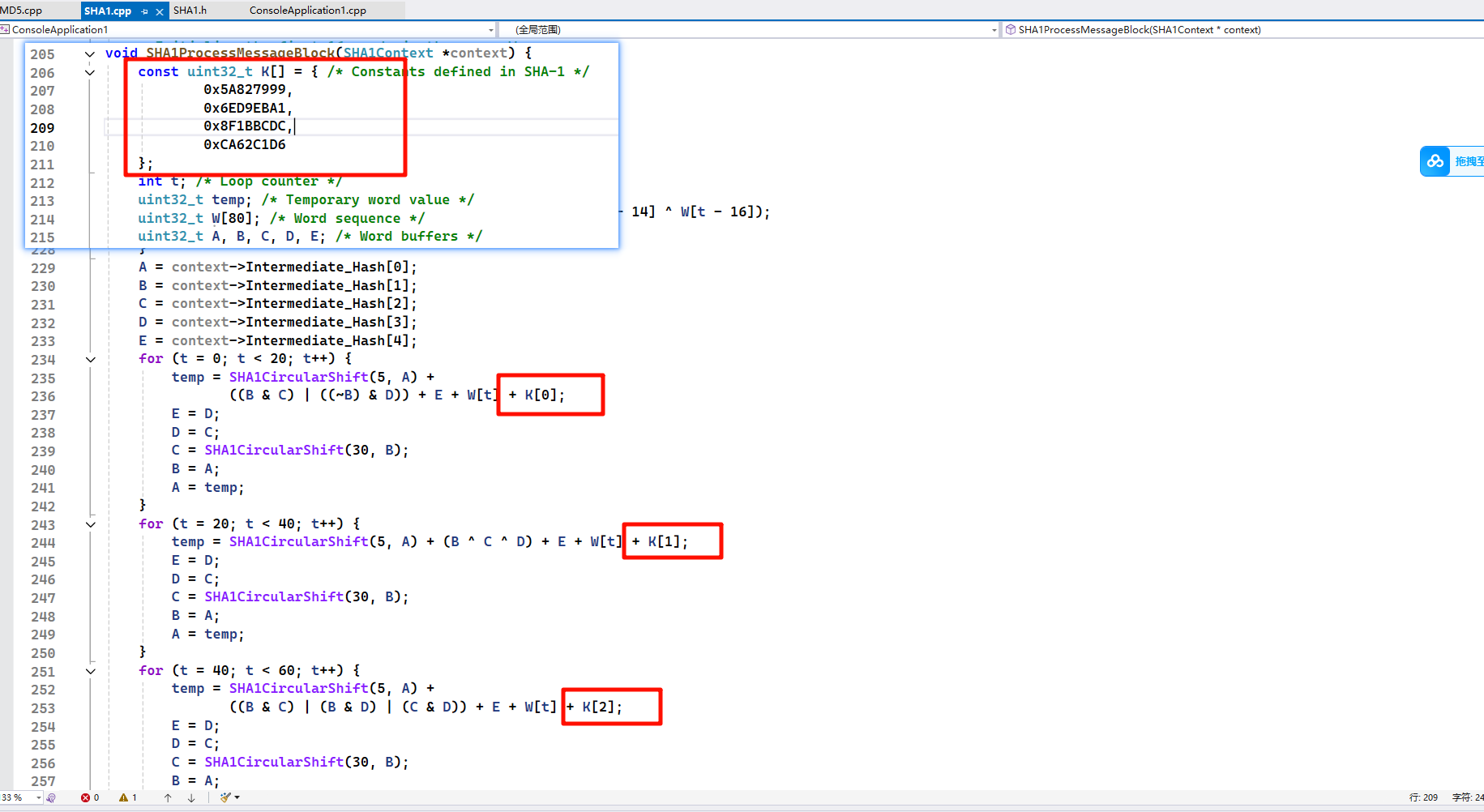
5、SHA1有五个初始化常量，前四个和MD5相同。多出来的一个初始化常量，就是结果比MD5多出来64bit的原因。因为这两个算法都是对初始化常量进行一系列的运算之后，得到摘要结果，初始化常量多64bit，结果自然多64bit。

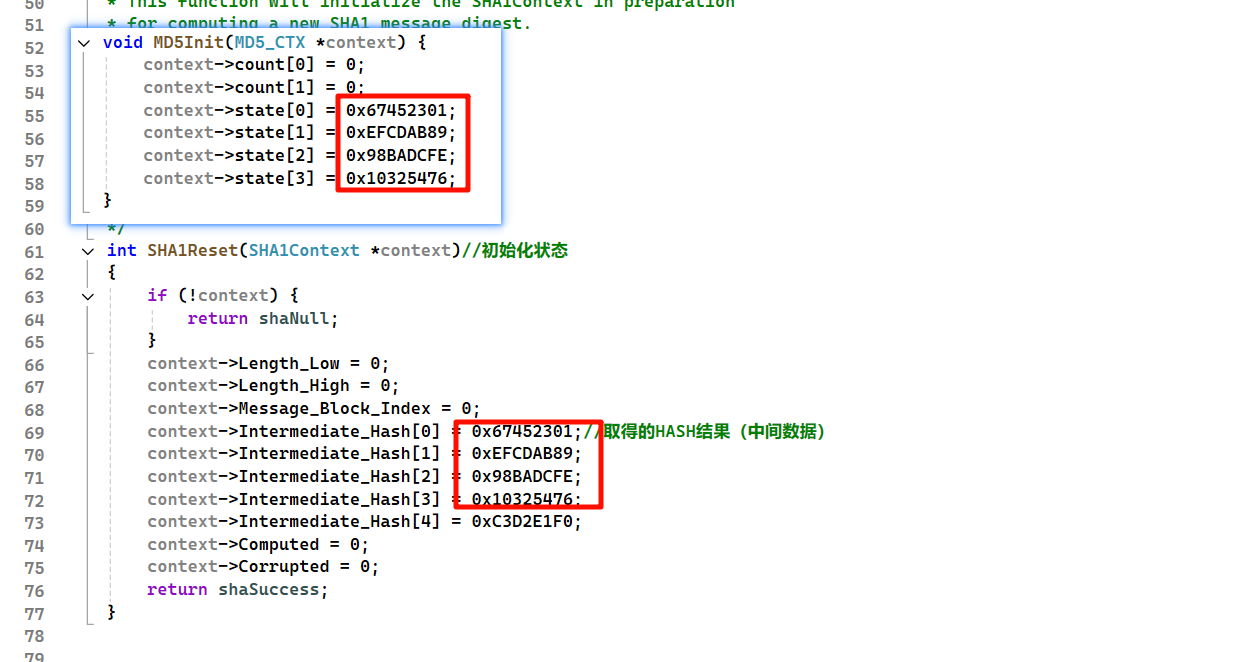
因为SHA1是大端字节序，所以计算之后是将初始化常量直接拼接，MD5是小端字节序，将计算之后的初始化常量倒序拼接

SHA1的明文长度必须小于 2^64

源码分析

从使用上来说，MD5和SHA1的使用方法大差不差。

MD5init 和 SHA1Reset 初始化

MD5Update 和 SHA1Input 压入数据

MD5Final 和 SHA1Result 计算结果

写法都是一样的，只有传入的位数不一样，给到的result是结果位数，MD5是128bit，SHA1是160位

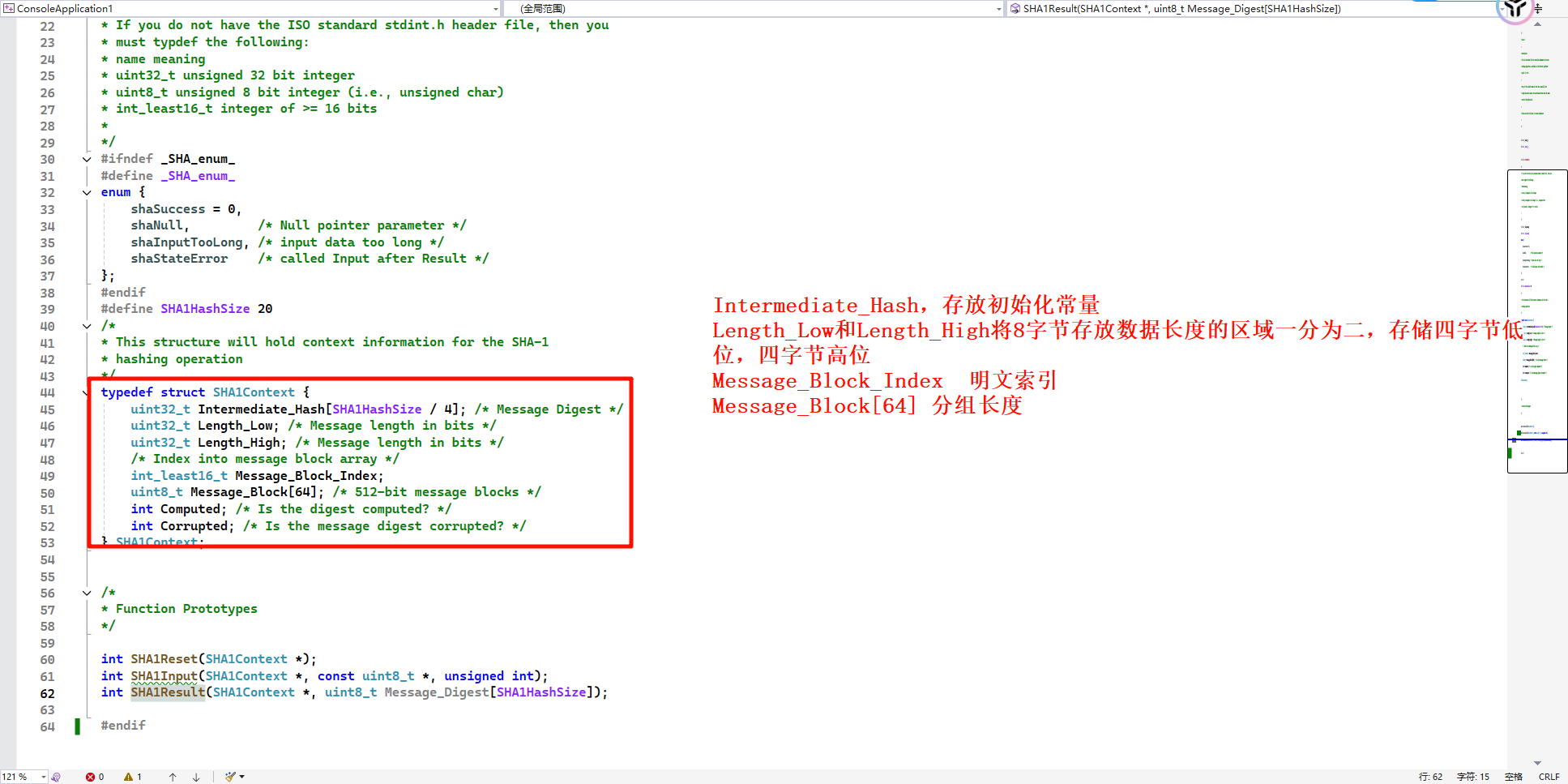
SHA1Reset函数

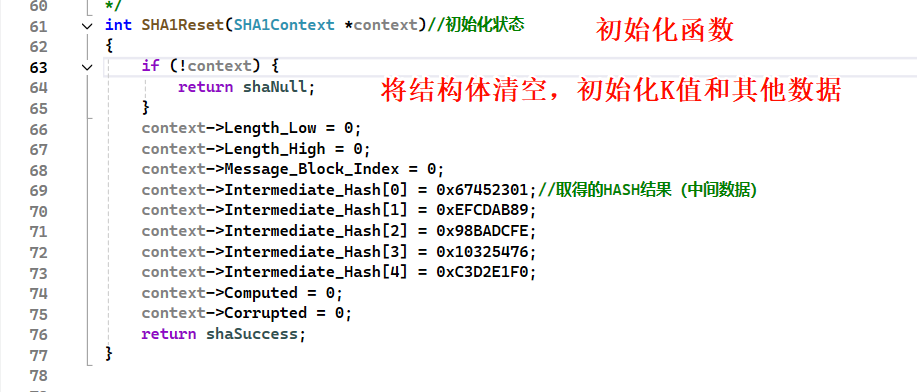
SHA1Input方法：将明文数据压入数组，如果数组满64字节进入 SHA1ProcessMessageBlick 方法计算。和MD5Update同理

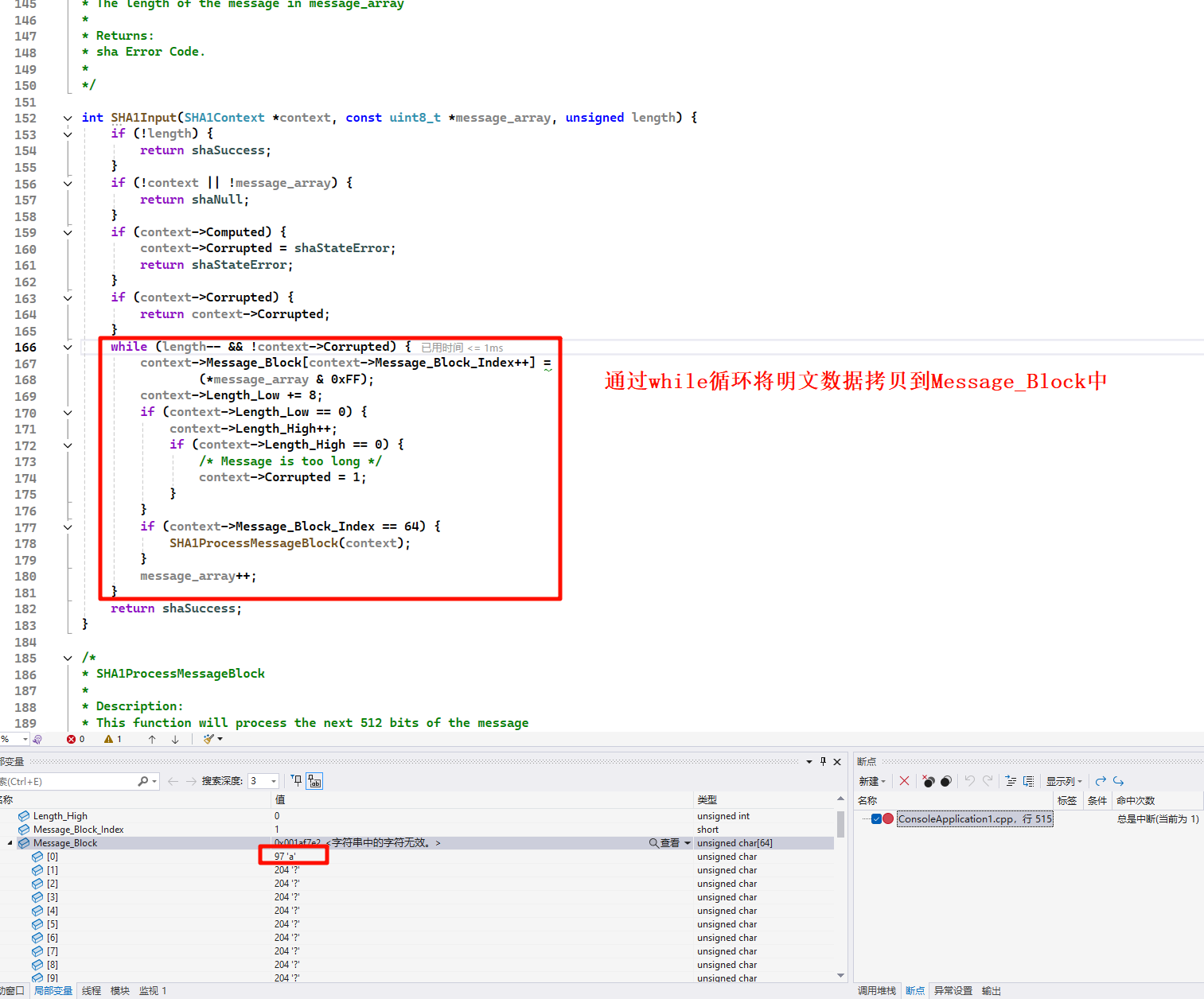
SHA1Result方法。利用传入值做返回值，Message_Digest运算后就是最终结果，将五个初始化常量拼接起来就是Message_Digest。进入SHA1Result时不满512bit，进入 SHA1PadMessage 进行填充

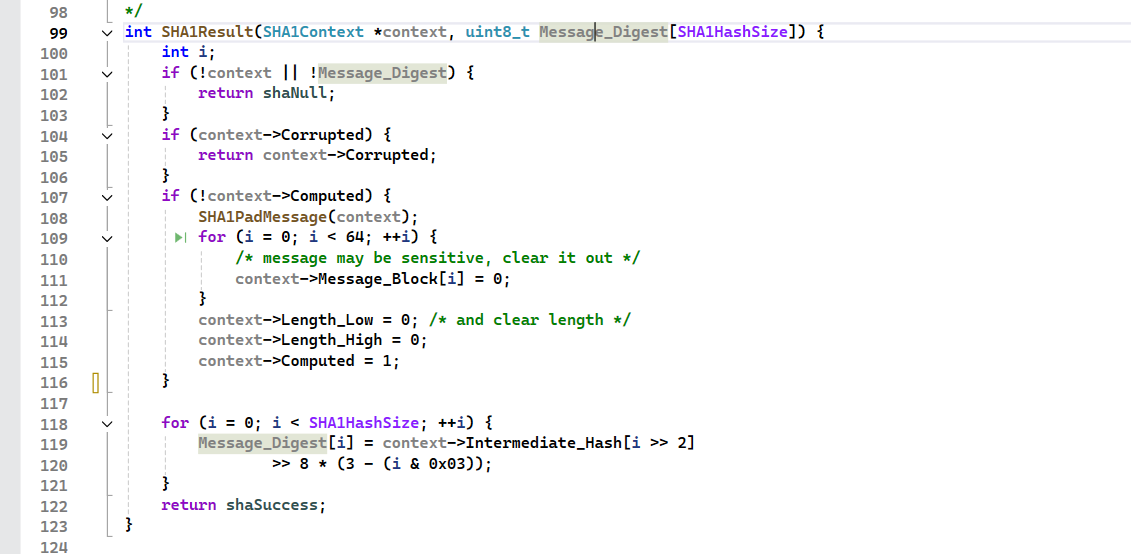
SHA1PadMessage

嘴瓢了，是右移

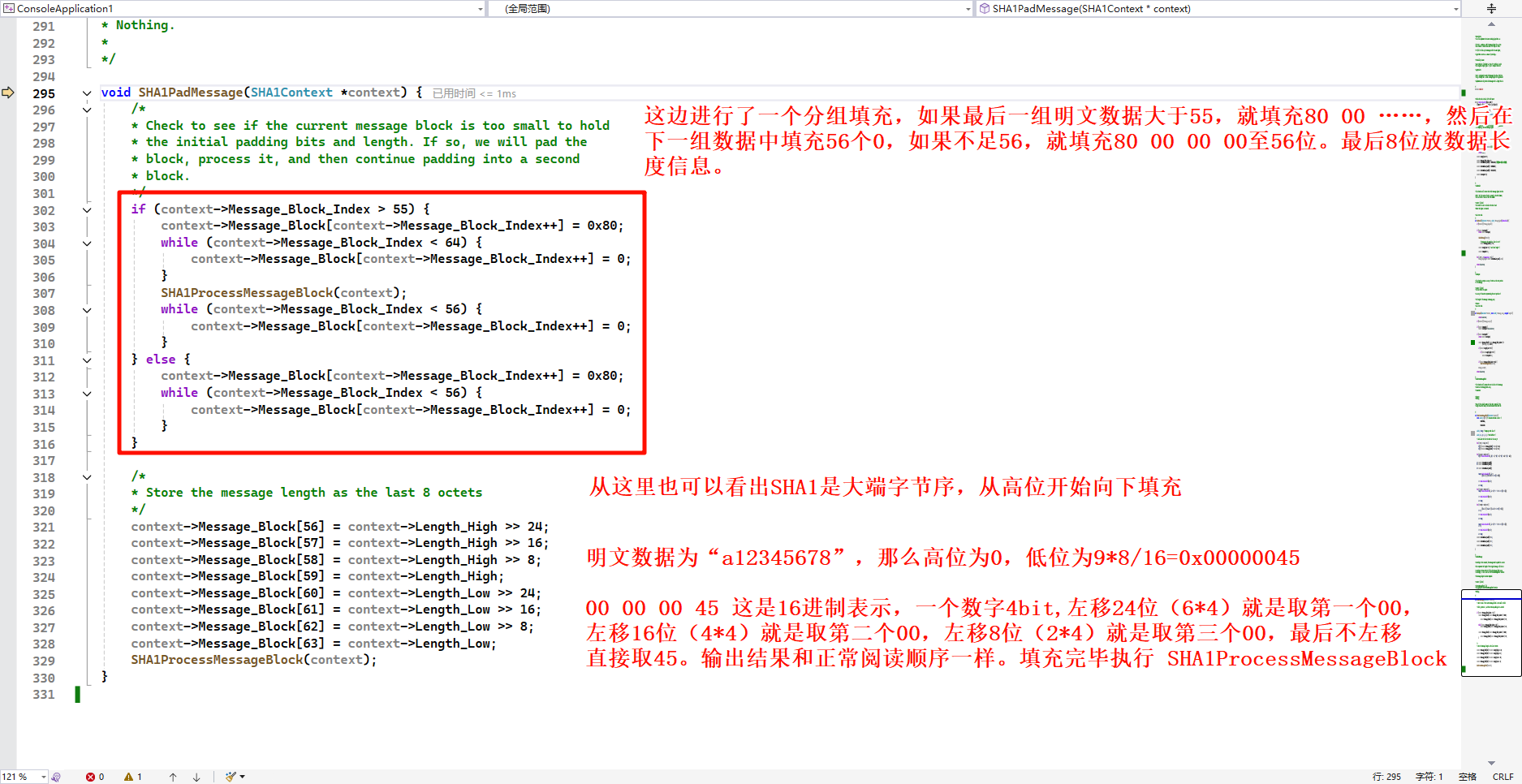
SHA1ProcessMessageBlock 计算方法，对填充成512的分组进行计算

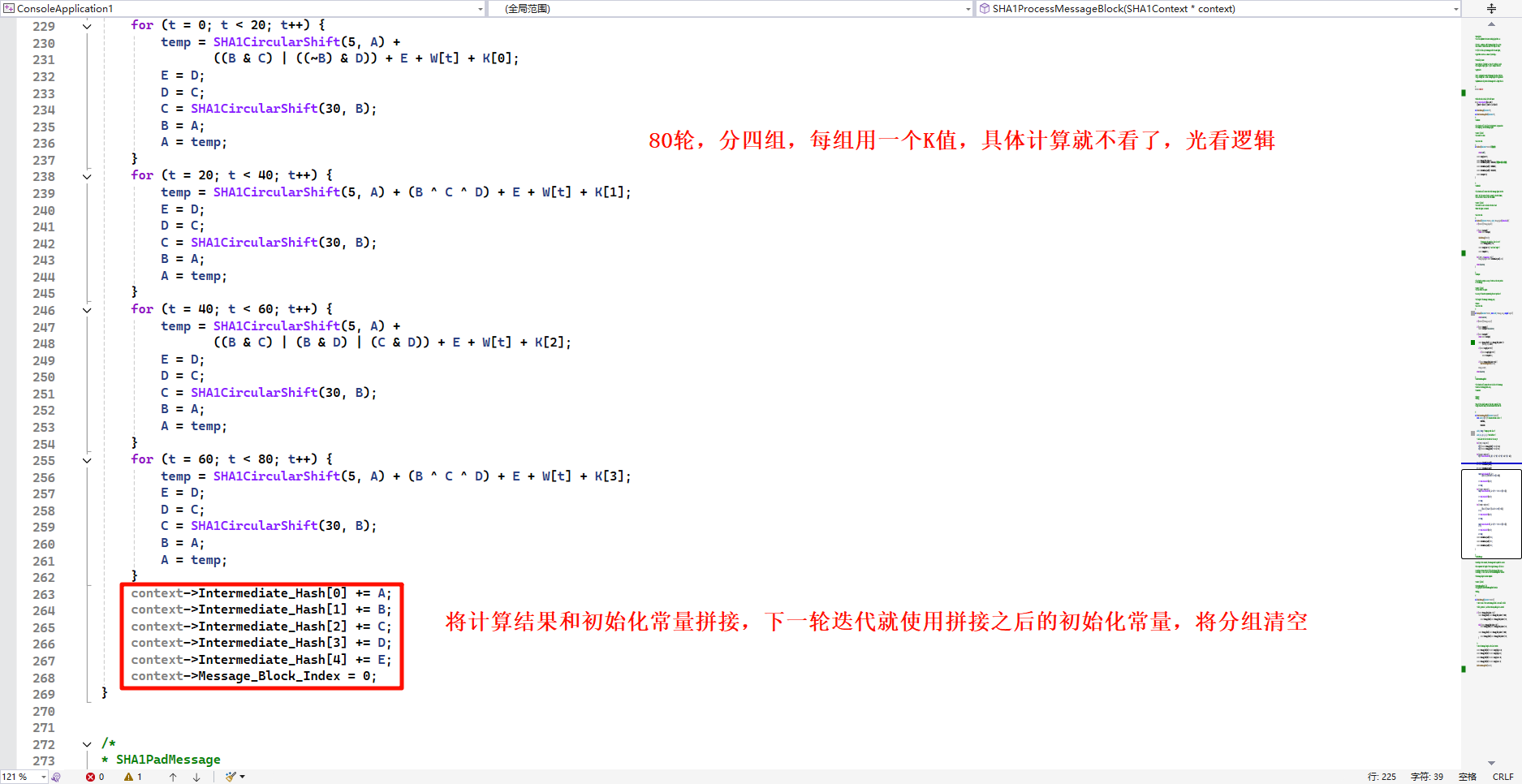
哈希算法特征识别

MD5

a）四个初始化常量
A = 0x67452301
B = 0xEFCDAB89
C = 0x98BADCFE
D = 0x10325476

b）K表64个
K1 = 0xd76aa478
K2 = 0xe8c7b756
K3 = 0x242070cb

c）结果输出长度
输出长度为16字节，或者说是32个16进制数，128bit

SHA1

a)五个初始化常量（前四个和MD5相同）
A = 0x67452301
B = 0xEFCDAB89
C = 0x98BADCFE
D = 0x10325476
E = 0xC3D2E1F0

b)K表 4个
只有四个K值，每20轮用一个K值
K1 = 0x5a827999
K2 = 0x6ed9eba1
K3 = 0x8f1bbcdc
K4 = 0xca62c1d6

c)输出长度为20字节，40个十六进制数，160bit

SHA256

a)八个初始化常量
A = 0x6A09E667;
B = 0xBB67AE85;
C = 0x3C6EF372;
D = 0xA54FF53A;
E = 0x510E527F;
F = 0x9B05688C;
G = 0x1F83D9AB;
H = 0x5BE0CD19;

b)K表 64个，每轮一个K值，也就是说一个循环64次，数据扩充到64组
K1 = 0x428a2f98
K2 = 0x71374491
K3 = 0xb5c0fbcf
K4 = 0xe9b5dba5

c)输出长度为32字节，64个十六进制数，256bit

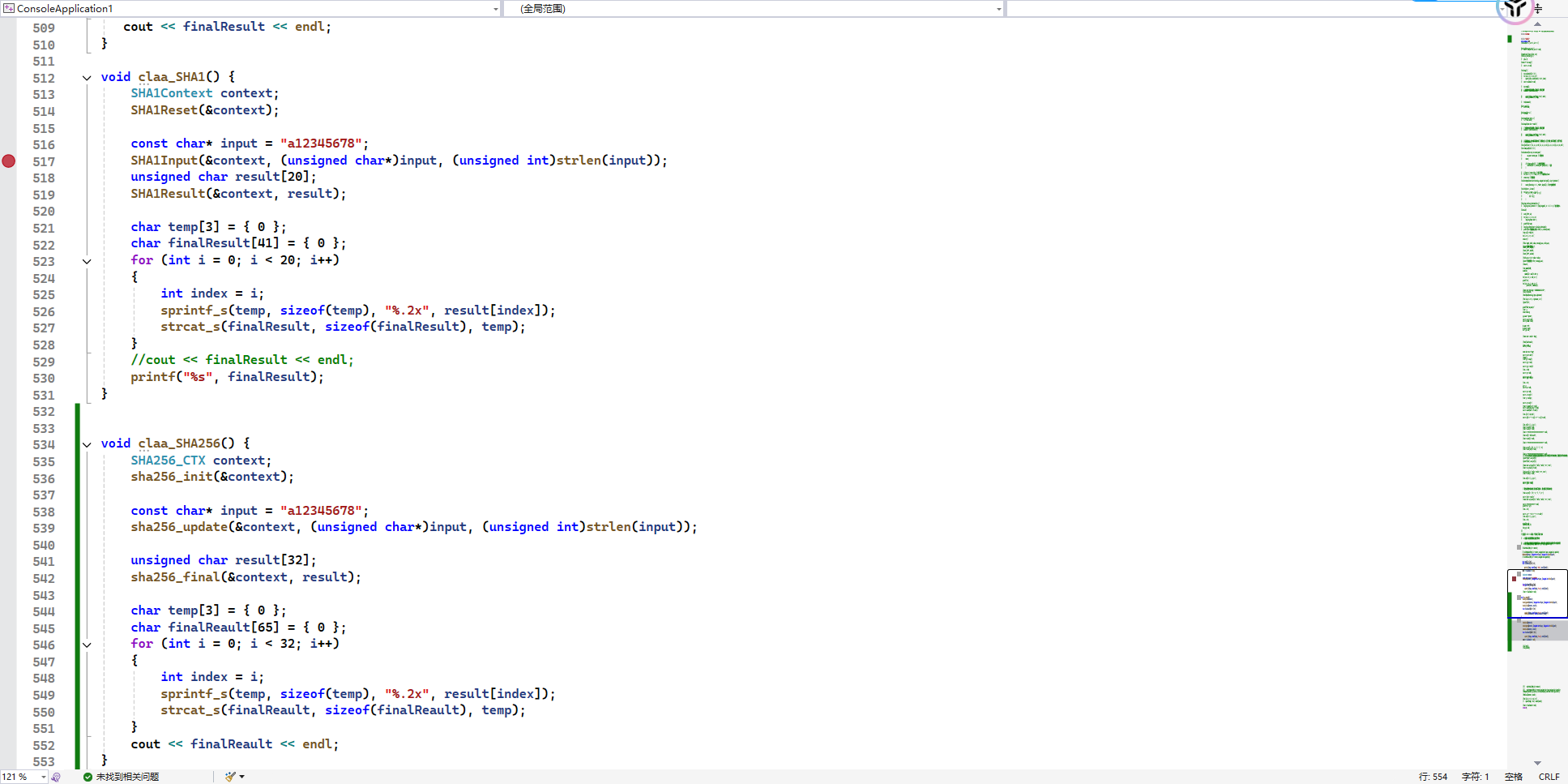
SHA256的一些方法和SHA1简直就像一个模子的东西

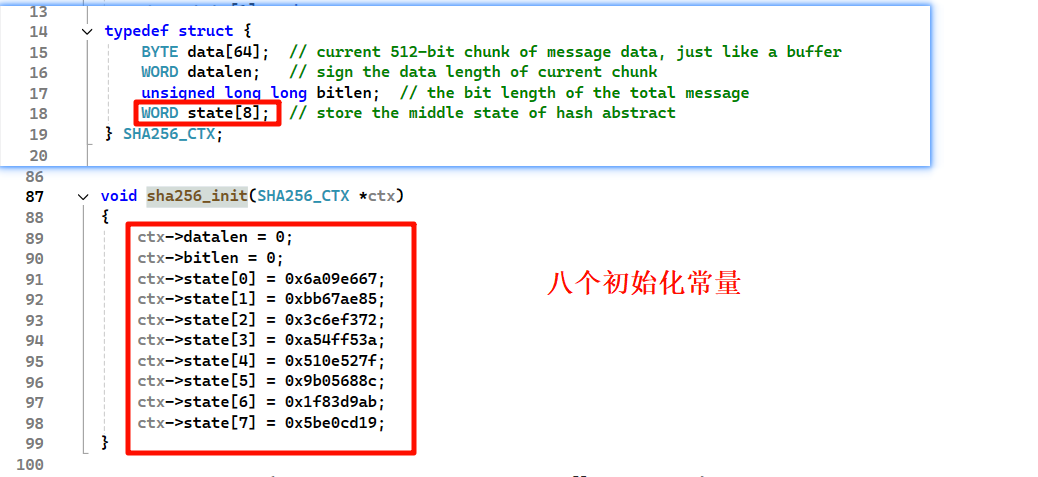
update同样是压入数据的方法，如果足够512字节，进入加密方法，不足512压入数组，等待下一步处理。SHA256的分组同样是512bit

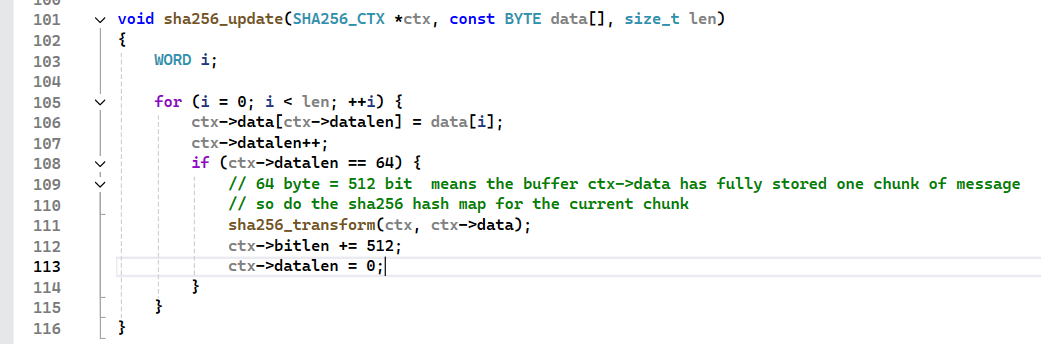
final同理

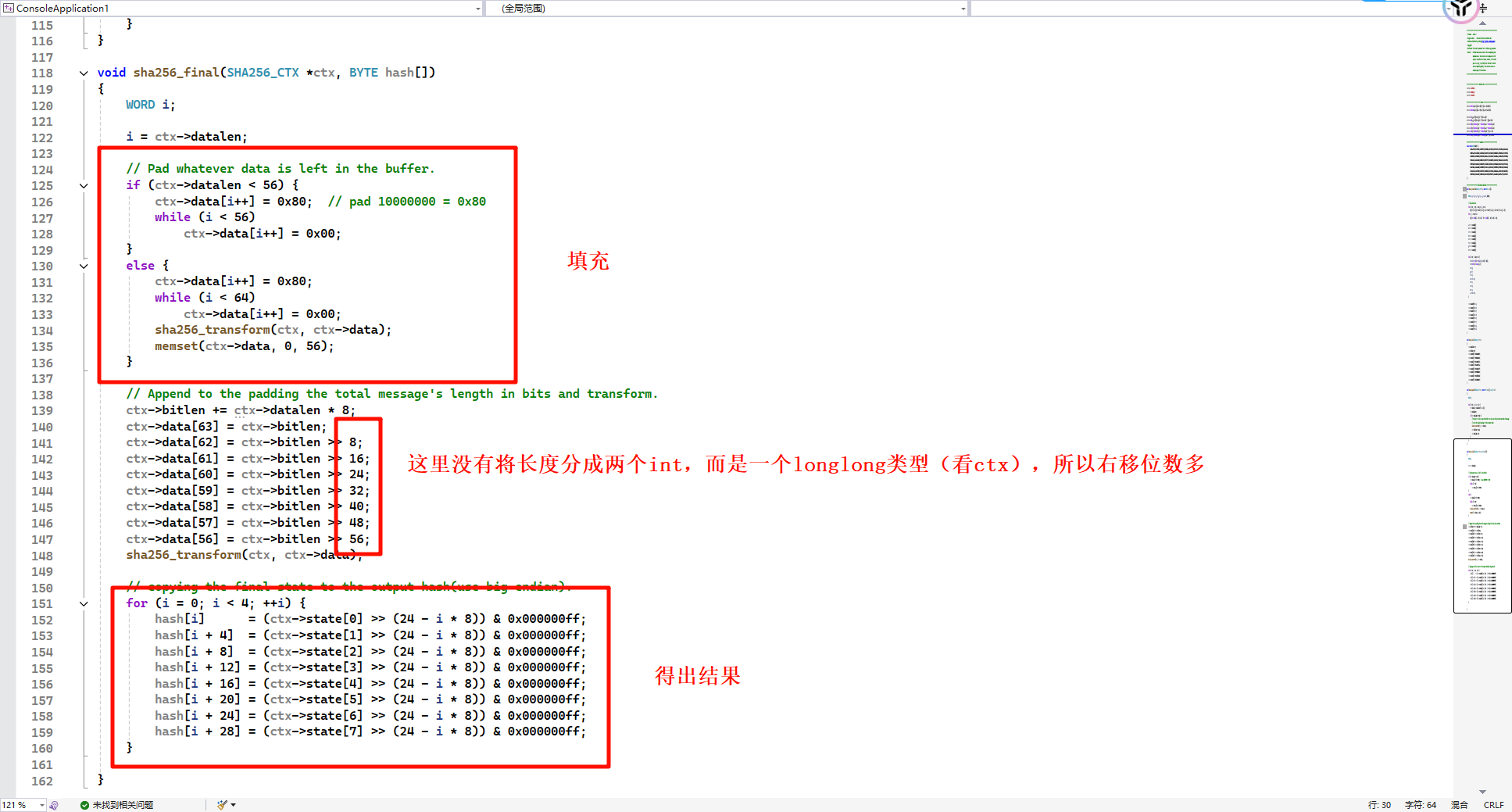
加密方法，需要注意的是和SHA1不同，SHA256是扩充到64组，而非扩充64组（共80组），因为64个K值，循环64次，自然总共64组。

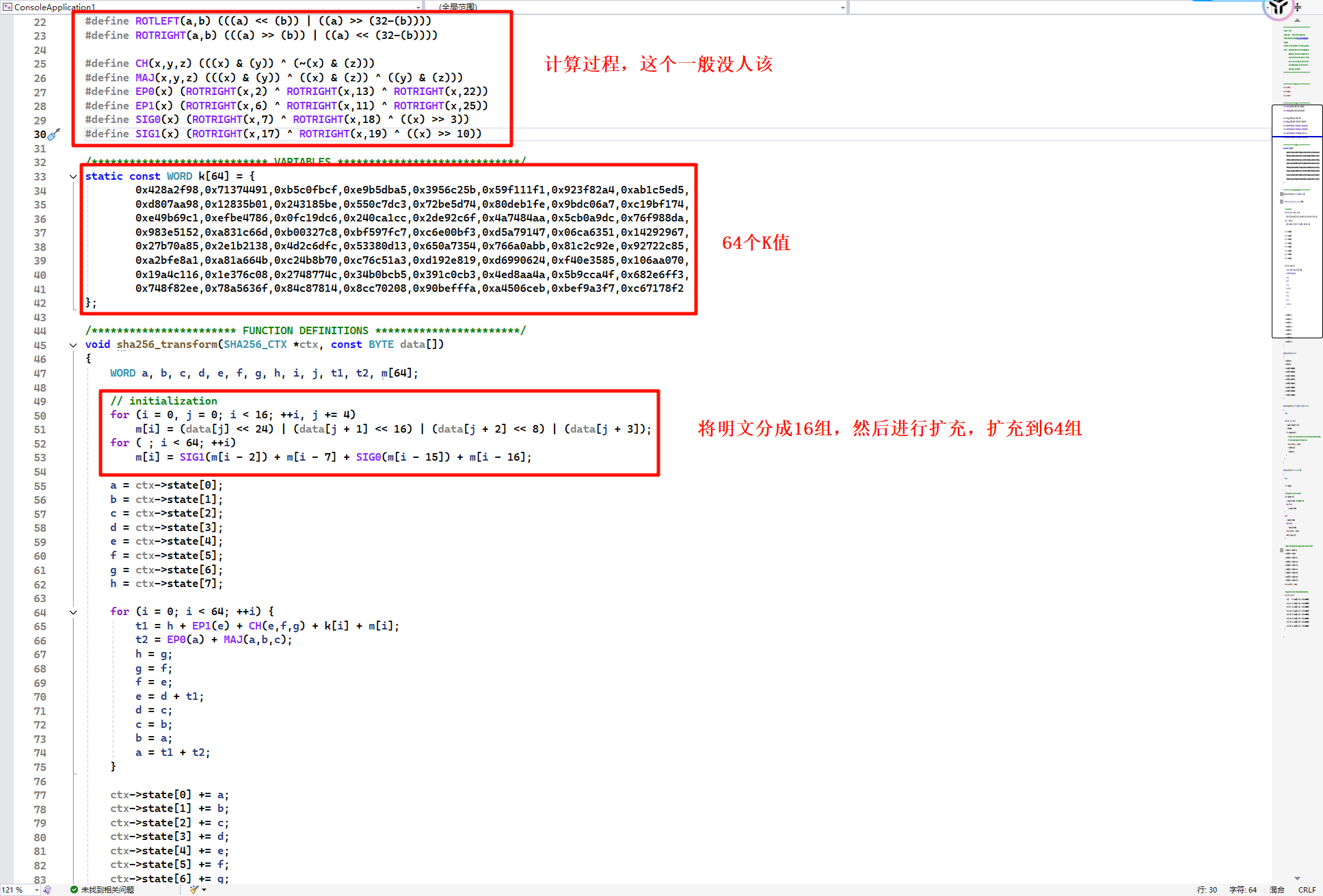
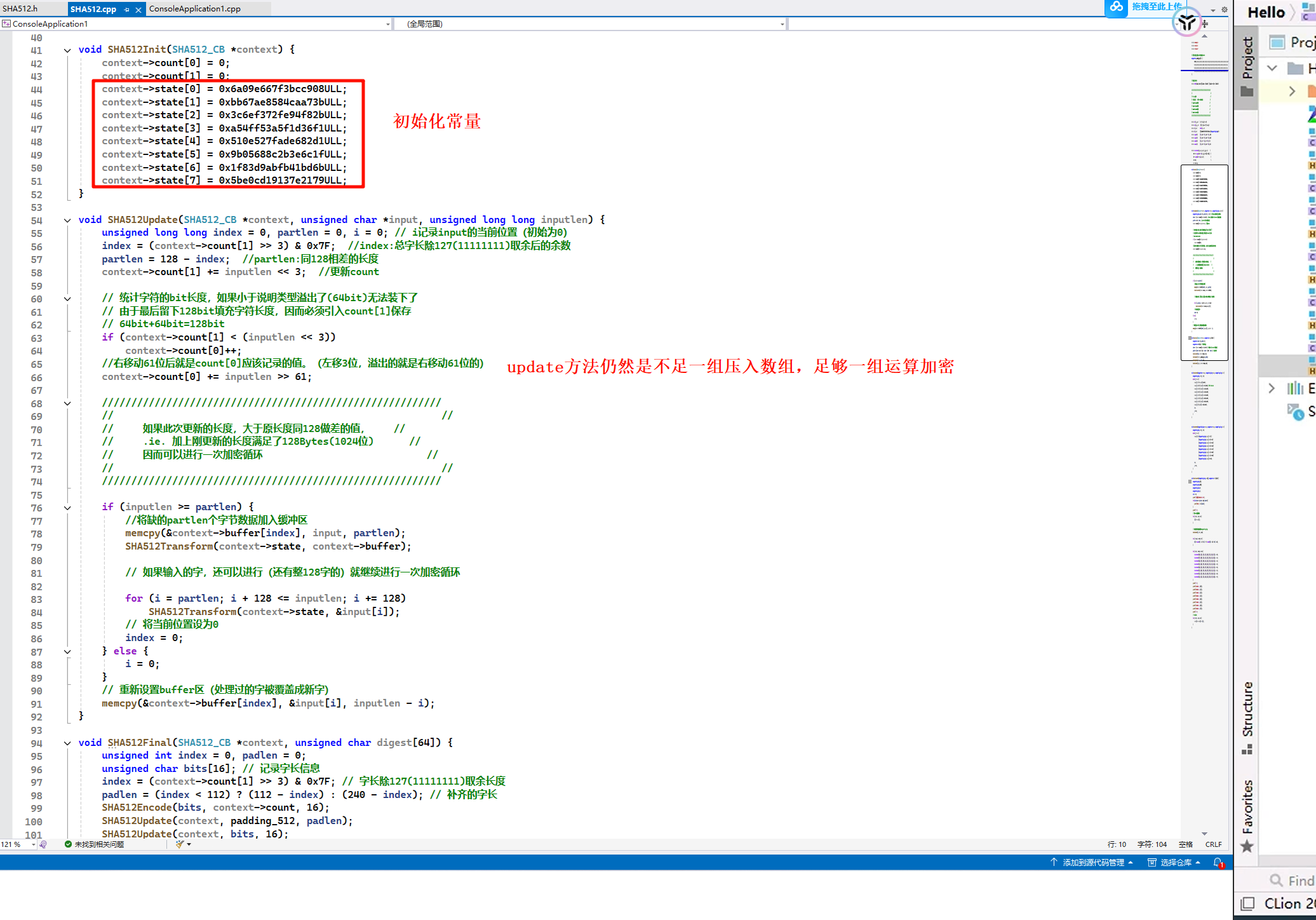
SHA512

a)初始化常量8个，IDA反编译时有时显示为16个，因为初始化常量比其他的长一半
	而且八个初始化常量，前半部分和SHA256是一样的
A = 0x6A09E667f3bcc908;
B = 0xBB67AE8584caa73b;
C = 0x3C6EF372fe94f82b;
D = 0xA54FF53A5f1d36f1;
E = 0x510E527Fade682d1;
F = 0x9B05688C2b3e6c1f;
G = 0x1F83D9ABfb41bd6b;
H = 0x5BE0CD19137e2179;

b)K表 80 个，每轮1个K值，80轮
K1 = 0x428a2f98d728ae22
K2 = 0x7137449123ef65cd
K3 = 0xb5c0fbcfec4d3d2f
K4 = 0xe9b5dba58189dbbc

c)输出长度为64字节，或者说128个十六进制数，共512bit

SHA512的明文分组是1024bit

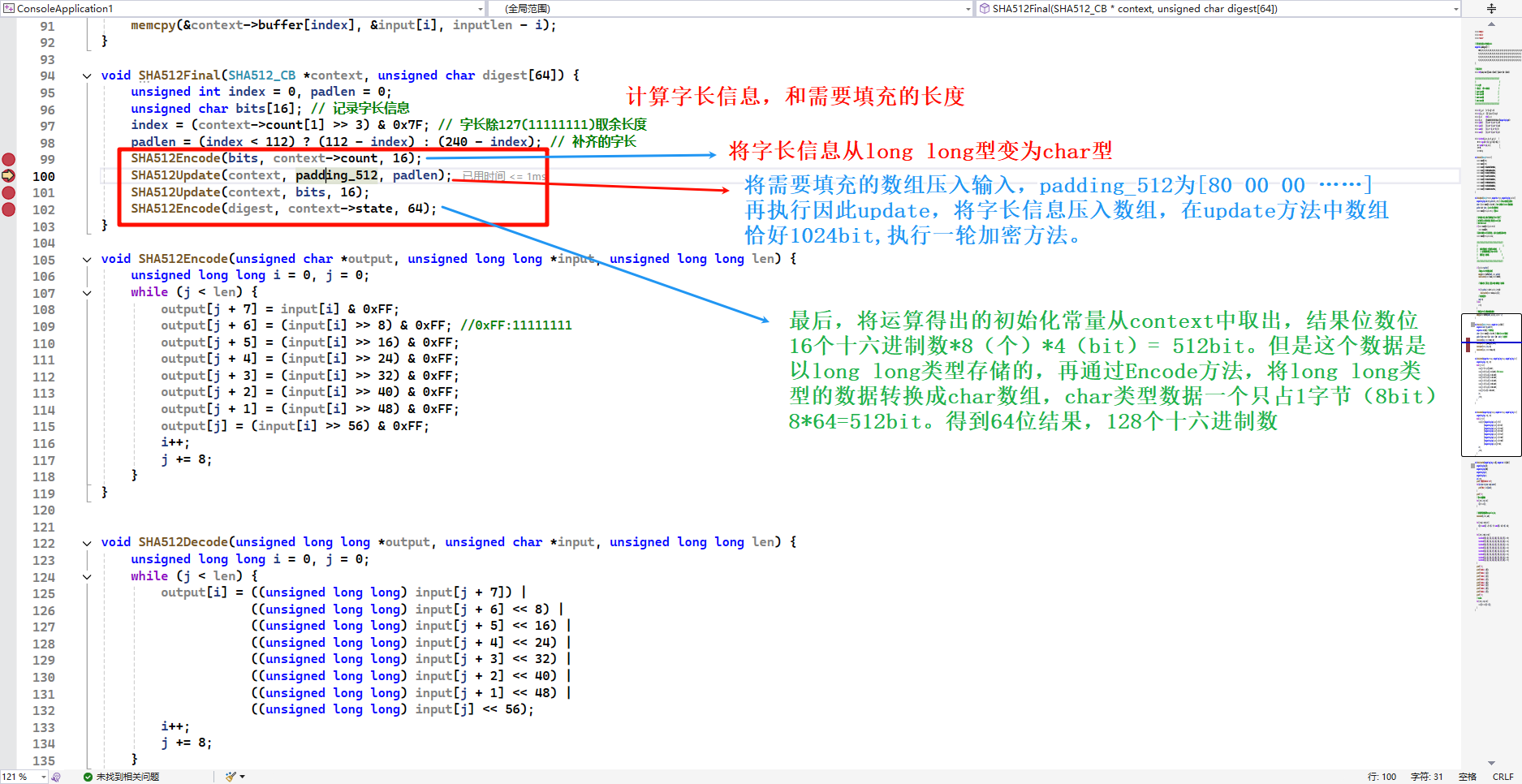
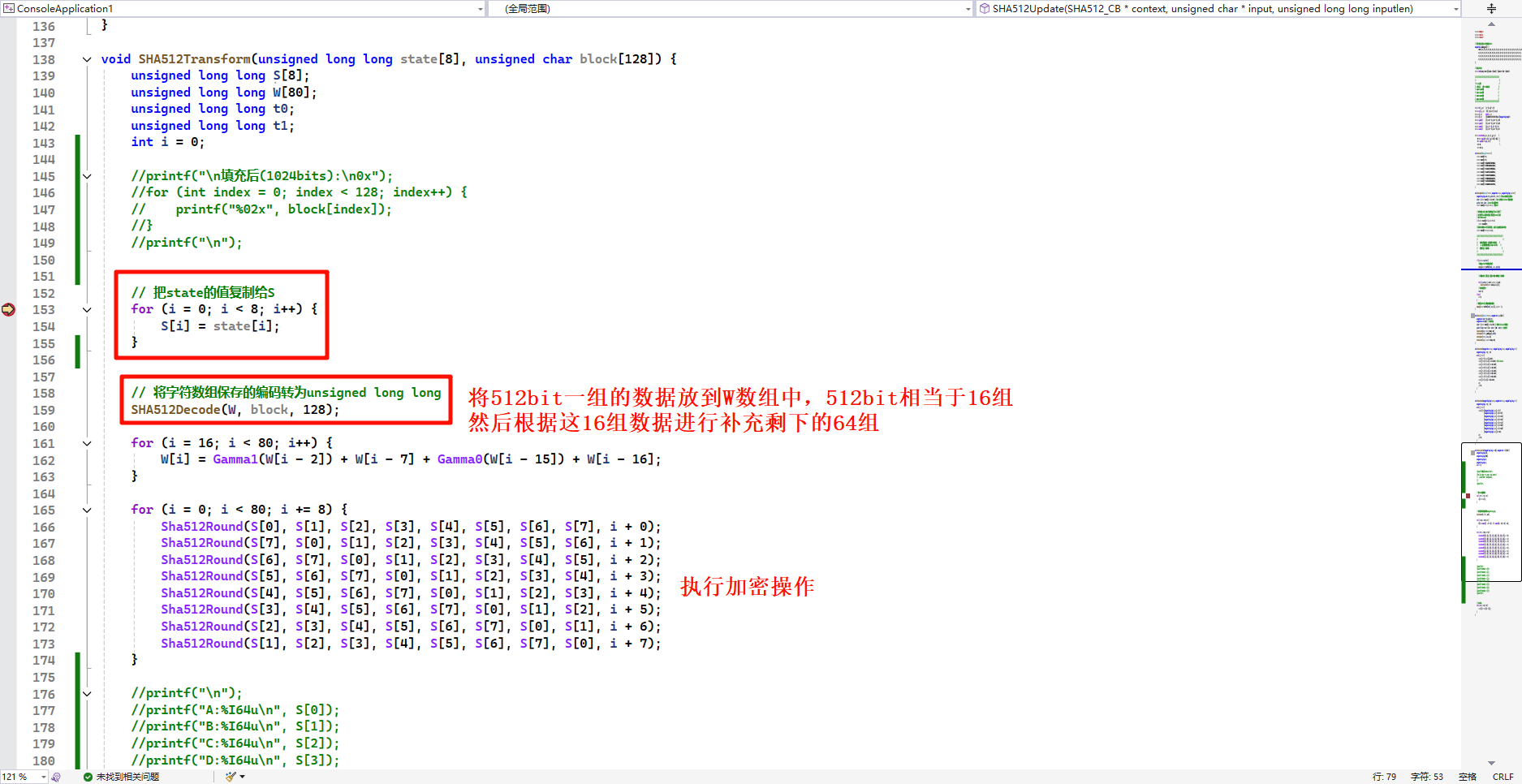
final方法

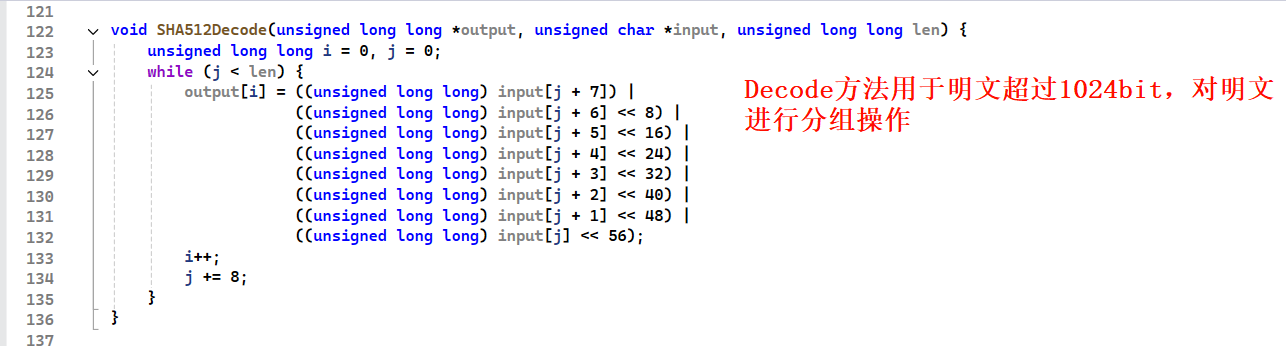
SHA512Decode方法

SHA512Transform

MAC

所谓MAC算法，其实就是两次加盐，两次hash的一种hash算法

以HmacMD5为例

1.密钥扩展
	a、密钥a12345678转成hex编码
		61 31 32 33 34 35 36 37 38
	b、然后填充0，让密钥长度达到算法分组长度，MD5就是512bit
		61 31 32 33 34 35 …… 00 00
	c、如果密钥超过分组长度，先计算一次，再填充
		16字节 + 00 …… 00
		
2、扩展后的密钥与0x36异或（同0异1）
	00 11 01 10(0x36)
	01 10 00 01(0x61)
	异或 01 01 01 11(0x57)
	计算结果：
	57 07 04 05 02 03 00 01 0e 36 36 …… 36 36
	
3、异或后的数据与明文数据（Message）级联（拼接）
	57 07 04 05 02 03 00 01 0e 36 36 …… 36 36 61 31 32 33 34 35 36 37 38

例：key为 a12345678

明文：demolist

key的hex形式：61 31 32 33 34 35 36 37 38

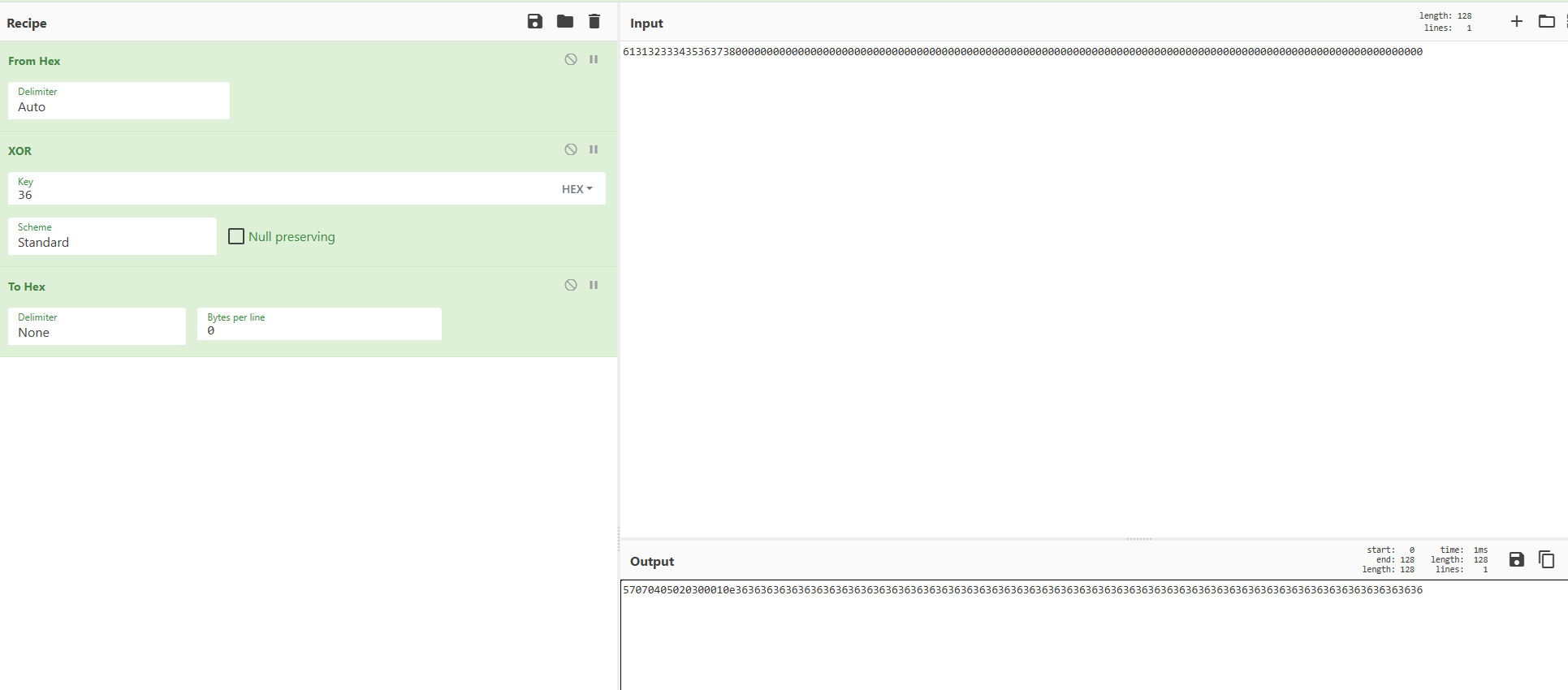
扩展到分组长度的key ：61313233343536373800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

ipad之后的数据：57070405020300010e36363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636

这里使用的网站直接0x36即可，在代码中需要用 3636……3636 （与分组长度相同），来表示。

明文的hex形式：64656d6f6c697374

明文的hex和ipad之后的数据级联：57070405020300010e3636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363664656d6f6c697374

级联后的hash：d7e2b1dc88875afba0edb5b9ff3ad912

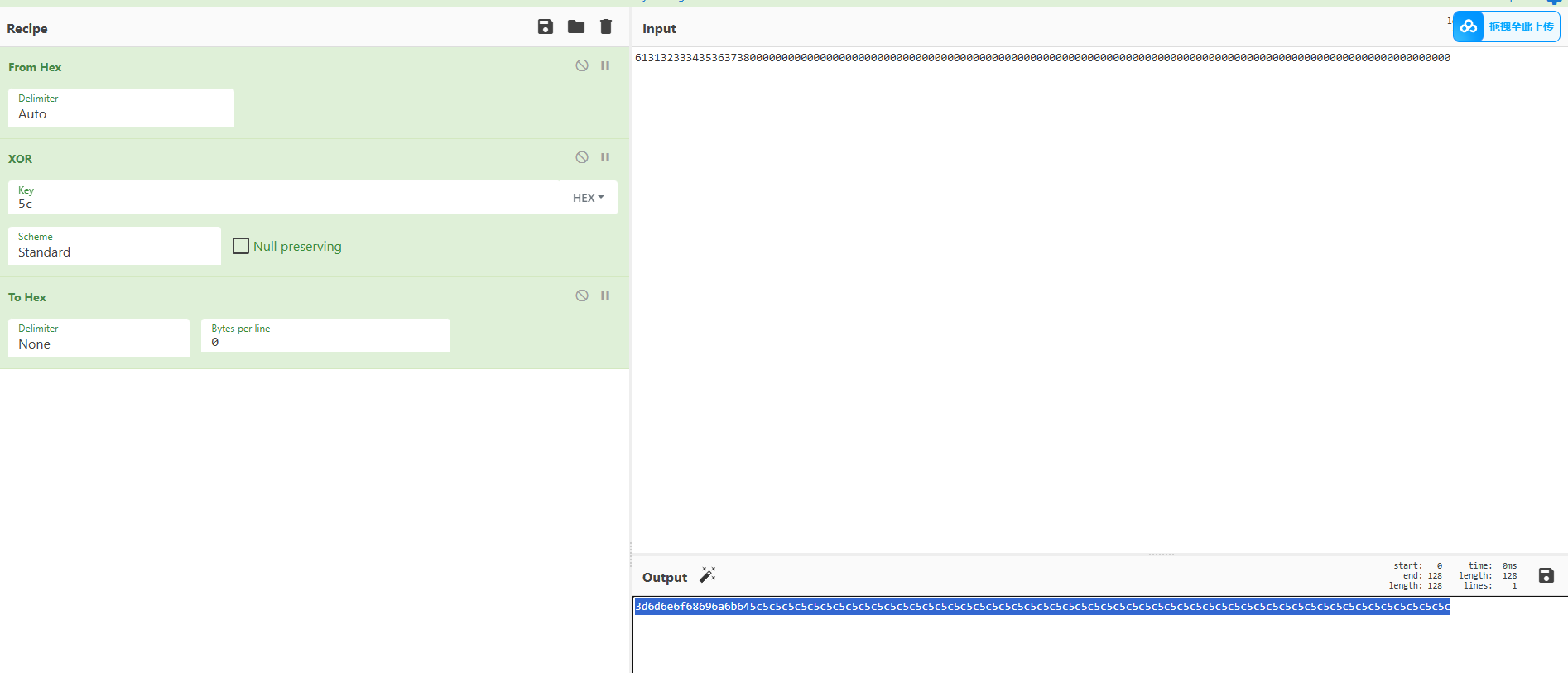
opad之后的数据：3d6d6e6f68696a6b645c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c

opad和hash结果进行级联（拼接）

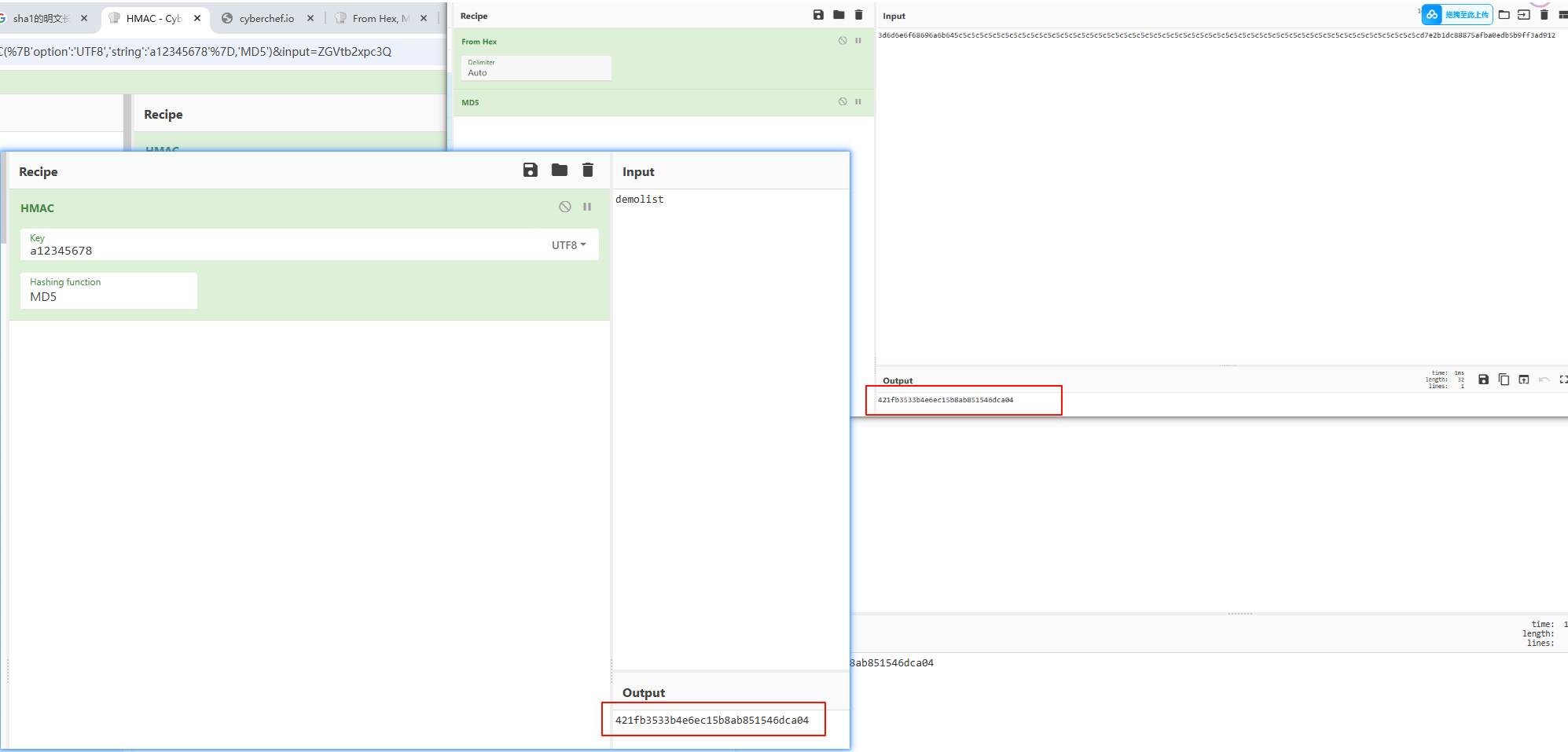
3d6d6e6f68696a6b645c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5cd7e2b1dc88875afba0edb5b9ff3ad912

再次hash就是最后结果：421fb3533b4e6ec15b8ab851546dca04

代码

从代码实现上来看，实现了MD5之后，再实现Hmac_MD5就简单了很多

在代码层面是直接从字节入手的，因此上文各种转换在代码中是不需要的

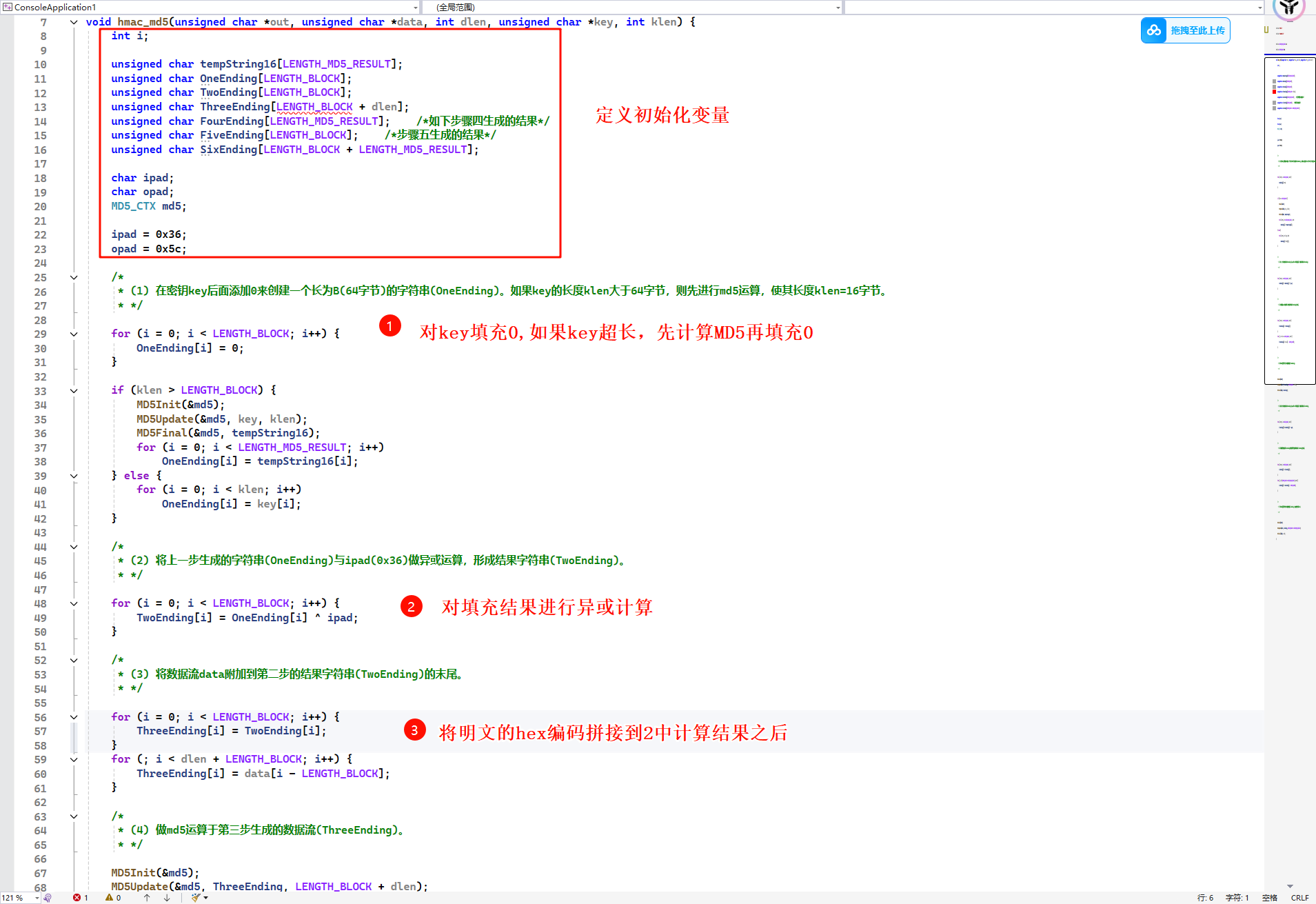
从代码上来看，是很难识别Hmac_MD5算法的，最多识别出来MD5算法，HMAC算法最明显的两个标志是 0x36 和 0x5c 这两个用来异或的。对应十进制数字是 54 92

DES

大佬链接：https://www.anquanke.com/post/id/177808#h3-5

之前已经介绍过DES不安全是因为密钥不唯一，64位的密钥只有56位参与运算，一个字符二进制的最后一位不参与运算。

不考虑填充方式，不考虑加密模式，不考虑IV值，输入明文8字节，输入密文8字节，输出结果8字节

密钥处理流程

假设有密钥：abcd1234
转换成二进制数据为
01100001 01100010 01100011 01100100 00110001 00110010 00110011 00110100

DES算法中有一个PC1表，根据这个表将密钥重新排列
initial_key_permutaion = [57, 49,  41, 33,  25,  17,  9,
                           1, 58,  50, 42,  34,  26, 18,
                          10,  2,  59, 51,  43,  35, 27,
                          19, 11,   3, 60,  52,  44, 36,
                          63, 55,  47, 39,  31,  23, 15,
                           7, 62,  54, 46,  38,  30, 22,
                          14,  6,  61, 53,  45,  37, 29,
                          21, 13,   5, 28,  20,  12,  4];
                          
替换结果为：0000000 0000011 1111111 1111111 0110011 0100010 0000000 0000000

然后将结果分成左右两部分C0,D0
C0 = 0000000 0000011 1111111 1111111
D0 = 0110011 0100010 0000000 0000000

key_shift = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
对C0和D0进行循环左移操作，左移位数按照key_shfit，得到C1-C16,D1-D16，这个循环左移位数是相对于Ci-1和Di-1来说的。
C1 = 0000000 0000111 1111111 1111110
D1 = 1100110 1000100 0000000 0000000
C2 = ……
D2 = ……

将Ci和Di进行合并
C1D1 = 0000000 0000111 1111111 1111110 1100110 1000100 0000000 0000000
C2D2 = ……

再根据PC2表进行重排，56bit长的CnDn留下 48 bit

PC2_Table = [14,17,11,24, 1, 5, 3,28,15, 6,21,10,
			23,19,12, 4,26, 8,16, 7,27,20,13, 2,
			41,52,31,37,47,55,30,40,51,45,33,48,
			44,49,39,56,34,53,46,42,50,36,29,32];
			
重排之后的CnDn就是子密钥，Kn
一共有16个子密钥。后续十六轮运算，每一轮用一个子密钥。
K1 = 000110100000001011101111111111000111000001110010

明文处理

假设有明文：abcd1234
转换成二进制数据：
01100001 01100010 01100011 01100100 00110001 00110010 00110011 00110100

根据IP表，对明文进行初始置换
IP_Table = [58, 50, 42, 34, 26, 18, 10,  2, 60, 52, 44, 36, 28, 20, 12,  4,
		   62, 54，46, 38, 30，22, 14,  6, 64，56，48, 40, 32, 24, 16,  8,
		   57，49，41, 33, 25，17,  9， 1, 59，51，43, 35, 27, 19, 11,  3,
		   61, 53, 45, 37, 29, 21, 13,  5, 63, 55, 47, 39, 31, 23, 15,  7]
		   
重新排列之后：
00001111 11110000 10001000 01010101 00000000 11111111 00000000 01100110

将明文分成左右两半
L0和R0
L0 = 00001111 11110000 10001000 01010101
R0 = 00000000 11111111 00000000 01100110

将L0 R0进行16轮迭代
Ln = R(n-1)
Rn = L(n-1) xor f(R(n-1), Kn)

以n = 1 为例
L1 = R0 = 00000000 11111111 00000000 01100110
R1 = L0 xor f(R0, K1)


F函数详解
f函数传入了R0与K1，即第一个子密钥
R0 = 00000000 11111111 00000000 01100110
K1 = 000110100000001011101111111111000111000001110010

R0为32bit，K1为48bit，长度不同，没法按位异或
将R0拓展到48bit再进行异或，扩展使用E表
E_Table = [32,1,2,3,4,5,4,5,6,7，8, 9，
		  8,9,10,11,12,13,12, 13,14, 15,16,17,
		  16,17,18,19,20,21,20,21,22,23,24,25,
		  24,25,26,27,28,29,28,29,30,31,32,1];
		  
得到E(R0)
进行密钥混合 E(R0) ^ K1		(^相同为0，不同为1)
E(R0) = 000000 000001 011111 111110 100000 000000 001100 001100
K1 =    000110 100000 001011 101111 111111 000111 000001 110010
k1 + E(R0) = 000110 100001 010100 010001 011111 000111 001101 111110


算法核心：
将上一步的结果分成八份
B1 = 000110 
B2 = 100001
B3 = 010100
B4 = 010001
B5 = 011111 
B6 = 000111
B7 = 001101
B8 = 111110
把B1-B8的值当成索引，在S1-S8盒中取值，规则如下：
以B1为例，值为000110，将他分成 0 0011 0，得到
i = 00 即 0 （首尾拼接）
j = 0011 即 3
在S1盒中找到第0行，第三列的值——1


S1 = [14,  4, 13,  1,  2, 15, 11,  8,  3, 10,  6, 12,  5,  9,  0,  7,
       0, 15,  7,  4, 14,  2, 13,  1, 10,  6, 12, 11,  9,  5,  3,  8,
       4,  1, 14,  8, 13,  6,  2, 11, 15, 12,  9,  7,  3, 10,  5,  0,
      15, 12,  8,  2,  4,  9,  1,  7,  5, 11,  3, 14, 10,  0,  6, 13];

S2 = [15,  1,  8, 14,  6, 11,  3,  4,  9,  7,  2, 13, 12,  0,  5, 10,
       3, 13,  4,  7, 15,  2,  8, 14, 12,  0,  1, 10,  6,  9, 11,  5,
       0, 14,  7, 11, 10,  4, 13,  1,  5,  8, 12,  6,  9,  3,  2, 15,
      13,  8, 10,  1,  3, 15,  4,  2, 11,  6,  7, 12,  0,  5, 14,  9];

S3 = [10,  0,  9, 14,  6,  3, 15,  5,  1, 13, 12,  7, 11,  4,  2,  8,
      13,  7,  0,  9,  3,  4,  6, 10,  2,  8,  5, 14, 12, 11, 15,  1,
      13,  6,  4,  9,  8, 15,  3,  0, 11,  1,  2, 12,  5, 10, 14,  7,
       1, 10, 13,  0,  6,  9,  8,  7,  4, 15, 14,  3, 11,  5,  2, 12];

S4 = [ 7, 13, 14,  3,  0,  6,  9, 10,  1,  2,  8,  5, 11, 12,  4, 15,
      13,  8, 11,  5,  6, 15,  0,  3,  4,  7,  2, 12,  1, 10, 14,  9,
      10,  6,  9,  0, 12, 11,  7, 13, 15,  1,  3, 14,  5,  2,  8,  4,
       3, 15,  0,  6, 10,  1, 13,  8,  9,  4,  5, 11, 12,  7,  2, 14];

S5 = [ 2, 12,  4,  1,  7, 10, 11,  6,  8,  5,  3, 15, 13,  0, 14,  9,
      14, 11,  2, 12,  4,  7, 13,  1,  5,  0, 15, 10,  3,  9,  8,  6,
       4,  2,  1, 11, 10, 13,  7,  8, 15,  9, 12,  5,  6,  3,  0, 14,
      11,  8, 12,  7,  1, 14,  2, 13,  6, 15,  0,  9, 10,  4,  5,  3];

S6 = [12,  1, 10, 15,  9,  2,  6,  8,  0, 13,  3,  4, 14,  7,  5, 11,
      10, 15,  4,  2,  7, 12,  9,  5,  6,  1, 13, 14,  0, 11,  3,  8,
       9, 14, 15,  5,  2,  8, 12,  3,  7,  0,  4, 10,  1, 13, 11,  6,
       4,  3,  2, 12,  9,  5, 15, 10, 11, 14,  1,  7,  6,  0,  8, 13];

S7 = [ 4, 11,  2, 14, 15,  0,  8, 13,  3, 12,  9,  7,  5, 10,  6,  1,
      13,  0, 11,  7,  4,  9,  1, 10, 14,  3,  5, 12,  2, 15,  8,  6,
       1,  4, 11, 13, 12,  3,  7, 14, 10, 15,  6,  8,  0,  5,  9,  2,
       6, 11, 13,  8,  1,  4, 10,  7,  9,  5,  0, 15, 14,  2,  3, 12];

S8 = [13,  2,  8,  4,  6, 15, 11,  1, 10,  9,  3, 14,  5,  0, 12,  7,
       1, 15, 13,  8, 10,  3,  7,  4, 12,  5,  6, 11,  0, 14,  9,  2,
       7, 11,  4,  1,  9, 12, 14,  2,  0,  6, 10, 13, 15,  3,  5,  8,
       2,  1, 14,  7,  4, 10,  8, 13, 15, 12,  9,  0,  3,  5,  6, 11];
       
然后再将得到的数，转换成二进制用Bn接收
B1 = 1 = 0001
B2 = 13 = 1101
B3 = 12 = 1100
B4 = 1 = 0001
B5 = 6 = 0110
B6 = 2 = 0010
B7 = 1 = 0001
B8 = 8 = 1000
以此类推

最后将8个6bit的值转换成了8个4bit的值
S(K1+E(R0)) = 0001 1101 1100 0001 0110 0010 0001 1000

得到的结果进行P表的重排
P_Table = [16, 7,20,21,29,12,28,17, 1,15,23,26, 5,18,31,10,
		   2, 8,24,14,32,27, 3, 9,19,13,30, 6,22,11, 4,25]
		   
F = S(K1+E(R0)) = 1000 1010 0010 1101 0100 0001 1001 0010


继续将F的结果和L0进行异或（24行）(相同为0，不同为1)
L1 = R0 = 00000000 11111111 00000000 01100110
R1 = L0 xor f(R0, K1) = 00001111 11110000 10001000 01010101 
					^ 10001010 00101101 01000001 10010010
					= 10000101 11011101 11001001 11000111

如此一轮执行完毕，第一轮的L0和R0来自于明文，再往后就是使用上一轮的数据了
L1 = 00000000 11111111 00000000 01100110
R1 = 10000101 11011101 11001001 11000111
……………………
L16 = ……
R16 = ……

最后得到L16和R16，将二者调换，结果为 R16L16。
然后执行最后一步，根据FP表进行末置换（所谓魔置换就是初始计算的逆运算）

FP_Table = [40,  8, 48, 16, 56, 24, 64, 32, 39,  7, 47, 15, 55, 23, 63, 31,
		   38,  6, 46, 14, 54, 22, 62, 30, 37,  5, 45, 13, 53, 21, 61, 29,
		   36,  4, 44, 12, 52, 20, 60, 28, 35,  3, 43, 11, 51, 19, 59, 27,
		   34,  2, 42, 10, 50, 18, 58, 26, 33,  1, 41,  9, 49, 17, 57, 25]


经过置换之后的R16L16转换成十六进制就是最终结果

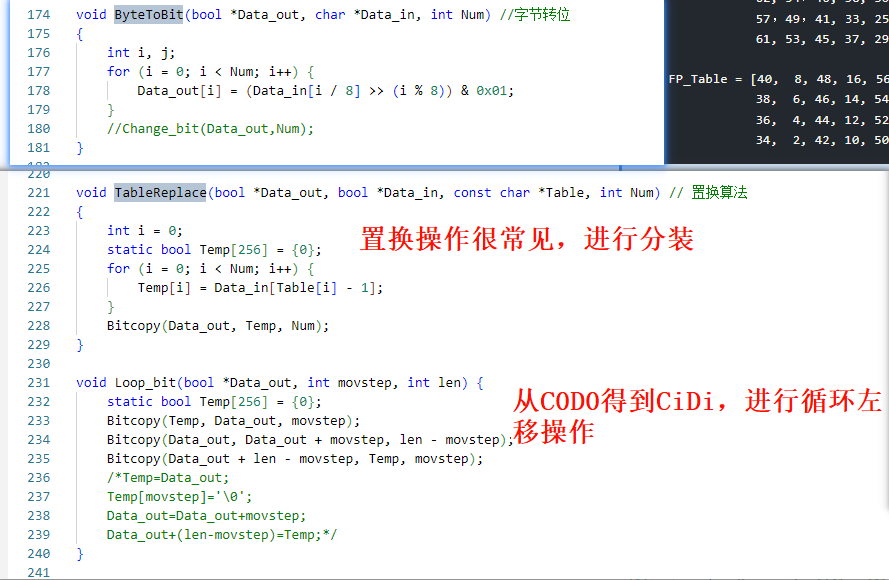
逆运算问题，FP表是IP表的逆运算
1
2
3
4
5
6
7
8
9
IP_Table = [58, 50, 42, 34, 26, 18, 10,  2, 60, 52, 44, 36, 28, 20, 12,  4,
		   62, 54，46, 38, 30，22, 14,  6, 64，56，48, 40, 32, 24, 16,  8,
		   57，49，41, 33, 25，17,  9， 1, 59，51，43, 35, 27, 19, 11,  3,
		   61, 53, 45, 37, 29, 21, 13,  5, 63, 55, 47, 39, 31, 23, 15,  7]

FP_Table = [40,  8, 48, 16, 56, 24, 64, 32, 39,  7, 47, 15, 55, 23, 63, 31,
		   38,  6, 46, 14, 54, 22, 62, 30, 37,  5, 45, 13, 53, 21, 61, 29,
		   36,  4, 44, 12, 52, 20, 60, 28, 35,  3, 43, 11, 51, 19, 59, 27,
		   34,  2, 42, 10, 50, 18, 58, 26, 33,  1, 41,  9, 49, 17, 57, 25]	   
为什么说是逆运算呢，就是将打乱的顺序再弄回去，比如，IP表第一个是58，明文进来二进制的第一个就去了第58位，FP表中的1在表中的第五十八个，就相当于，将在第58位的第一个二进制数又放了回去。以此类推

代码详解

留出来了四个方法，先看生成加密子密钥的方法

生成子密钥

SubKey是全局变量

加密过程

关于代码中没有体现L16和R16互换的这个问题：

这里的最后是不需要L16和R16颠 倒，因为每次运算都暗含了左右颠倒，这个运算并不是L一直在左边，而是让在左边的数叫Li，其实数据一直在左右变换，左边的数据变换到右边之后还要进行一个异或操作，从L1开始到L16，正好运算后完毕之后左边的数据在右边，右边的数据在左边，就不需要进行交换操作，而进行语言描述的的时候添加了这个状态，因此会说L16R16互换

循环加密完毕之后进行末置换转换成十六进制之后得到密文

解密和加密大差不差，DES的魔改点还是很多的，因为里面有很多表，比如明文的初始置换和末置换，这个修改不会影响安全性。还有S盒修改和白盒，白盒就是将密钥融入到算法里，一般是AES起步，但是结果还是标准的结果，只是拿不到密钥

分组加密的填充

DES数据分组密码，明文8个字节一组进行加密，当明文长度不足一个分组时就需要填充，以PCKS7为例

1、如果明文没有内容或者明文刚好是分组长度的整数倍，都需要填充一个分组，因此填充内容在8-64bit。

2、如果填充一个分组，那么填充内容是 08 08 08 08 08 08 08 08，明文七个字节填充 01，六个字节填充 02 02。

3、如果明文里有半个字节，先补0再填充，如果只有半个字节a，填充结果为

0a 07 07 07 07 07 07 07

加密模式

当明文长度超过一个分组时，就需要考虑加密模式了，不可能废那么大劲只加密8字符。加密模式包括 CBC CFB OFB CTR ECB。常用的有 CBC、ECB、CFB、OFB

ECB模式比较简单，就是每个分组单独加密，分组直接没有关联，可以分段解密，也可以通过替换某段密文，来达到替换明文的目的。这个不安全，之前也提到过。

CBC模式，引入了一个值，IV值，多了一个处理，就是这一轮的明文先和上一轮的进行异或，得到的结果再去运算，第一轮明文和IV值进行异或。这样确实安全了不是，但是是单线程，计算依赖上一轮结果，计算速度慢

CFB

CFB模式是一种流密码加密，不属于分组加密

CFB模式是先将IV值使用key作为密钥进行ECB模式的DES加密，得到的结果再作为IV值执行CBC模式

OFB

一个分组的OFB模式和CFB的流程是一样的，两个分组的OFB模式，第二个分组是明文和加密两次的IV值异或的结果

3DES

密钥24字节，等于3个DES的密钥，顾名思义嘛，执行三次DES，将密钥分成三段，第一个用于加密，第二个用于解密，第三个加密解密后的结果。

当前两段密钥相同时，3DES的结果就是一次单独的第三个密钥DES加密。

DES有安全问题时到AES出现之前的产物，增加DES密钥被穷举爆破的难度

AES

算法特点

AES算法还有个小名 Rijndael，Rijndael 算法本身分组长度是可变的，但是被确定为AES之后，分组长度只有128bit一种了

密钥长度为 128bit、192bit、256bit，分组长度为128bit。

AES128是10轮运算，AES192是12轮运算，AES256是14轮运算。DES 16轮

明文处理

先以最简单的ECB模式为例，假设明文为 abcd1234efgh1234 密钥为1234567887654321

明文state化

将明文转换成十六进制的形式，然后按照下表排列 61626364313233346566676831323334

61	31	65	31
62	32	66	32
63	33	67	33
64	34	68	34

数据竖向排列，明文密钥进行同样的处理

31	35	38	34
32	36	37	33
33	37	36	32
34	38	35	31

首先将state化之后的明文和种子密钥K进行异或，种子密钥就是用户输入的密钥，下面的子密钥是种子密钥拓展出来的，进行多少轮加密，扩展多少子密钥。

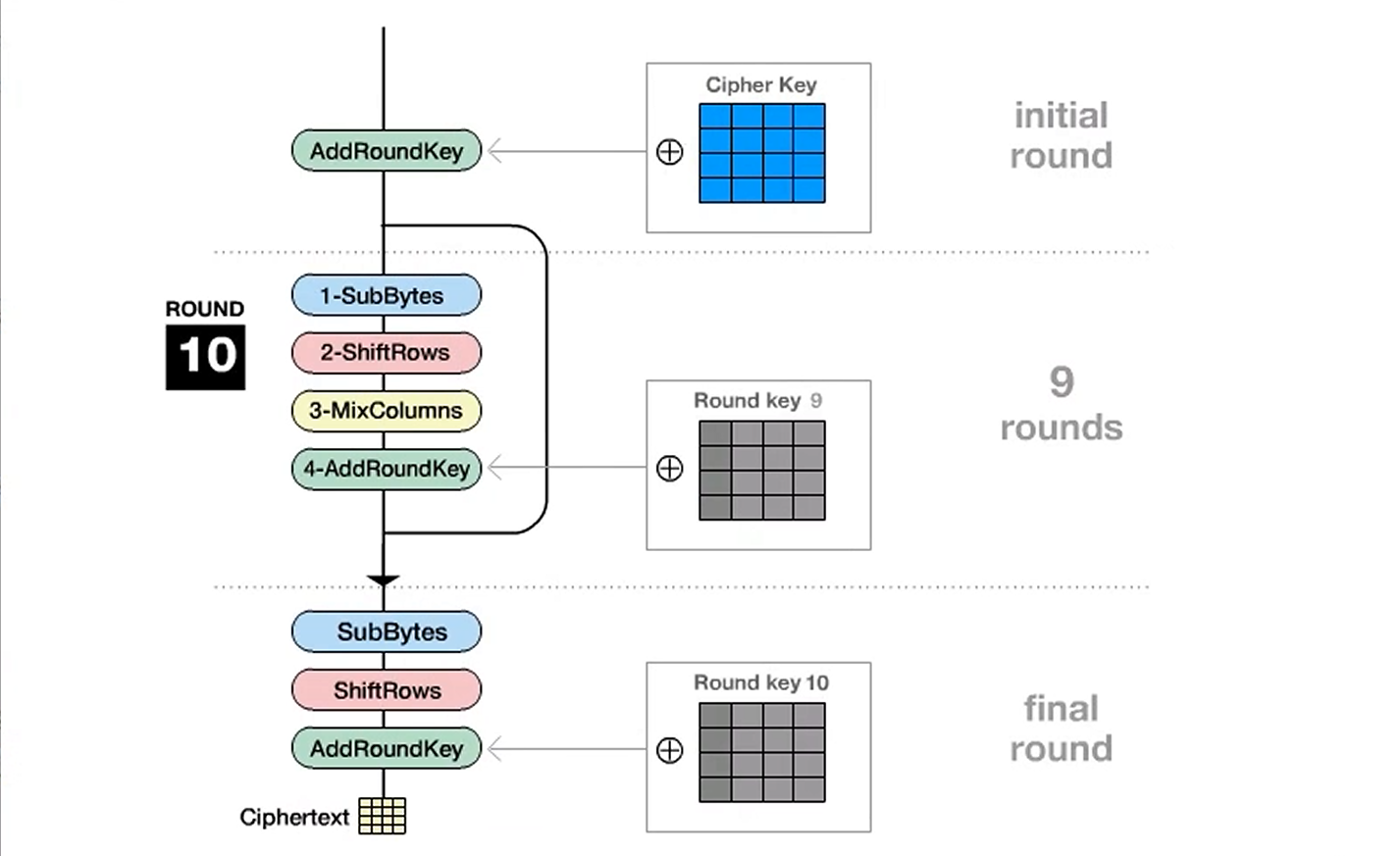
进行九轮运算，进行sbox替换，循环左移，列混合，state与子密钥K1-K9异或

前面提到过128bit的密钥进行10轮，还要一轮末运算，进行sbox替换，循环左移，state与子密钥K10异或。但是不进行列混合运算了。完毕之后得到密文

SubBytes(s-box替换)

根据state表中的十六进制数指示的去替换成表中的数据，值得注意的是DES加密的S盒有8个，AES加密的S盒只有这样一个，但是AES加密和解密用的不是同一个盒。但是两个盒是有着顺逆关系的。

61 31 65 31
62 32 66 32
63 33 67 33
64 34 68 34
例如61需要替换成，第七行第二列的 ef，剩余操作同理
ef c7 4d c7 
aa 23 33 23
fb c3 85 c3
43 18 45 18

ShiftRows(循环左移)

这个操作比较简单，针对state表中的数据进行操作，第一行不动，第二行左移一个，第三行左移两个，第四行左移三个。

以经过S盒替换的数据为例
ef c7 4d c7 
aa 23 33 23
fb c3 85 c3
43 18 45 18
经过左移变为
ef c7 4d c7
23 33 23 aa
85 c3 fb c3
18 43 18 45

这样就完事了

MixColumns(列混合变换)

https://blog.csdn.net/u012620515/article/details/49893905

https://bbs.kanxue.com/thread-147205.htm

这一步就相当复杂了

列混合存在一个 4*4 的矩阵

02 03 01 01
01 02 03 01
01 01 02 03
03 01 01 02

将左移之后的数据，这个矩阵的每一行与状态矩阵的每一列进行矩阵乘法运算，得到新的状态矩阵列。

伽罗瓦域运算

在矩阵乘法中，所有的加法和乘法运算都是在伽罗瓦域GF（2^8）中进行的。这个加法实际上就是异或运算，乘法有其他规则

乘01，返回结果是字段本身

乘02，相当于将二进制数据左移一位，如果最高位原本是1，左移之后需要与 0x1B （0001 1011）进行异或运算。如果不是一，直接左移一位

乘03，先进行乘02处理，然后将处理后的结果与原字节进行异或运算。

做运算的时候，将state状态矩阵的每一列，与列混合矩阵的每一行进行运算，得到新的列值。用坐标表示就是 (1，1)与(1，1)运算，(2，1)与(1，2)运算，(3，1)与(1，3)运算以此类推。

这个列混合运算的过程就有几个特征点，比如4*4的矩阵和 0x1B，0x80

AddRoundKey(异或)

将列混合变换后的结果和拓展过的Ki进行异或操作。

然后重复上述操作，一共执行九轮，第十轮没有列混合运算，得到密文

密钥编排

先将密钥的十六进制state化，然后以列为单位分为 Wi

Wi = Wi-1 ^ Wi-4，这个是一个拓展公式，当 i 能整除 4 的时候，则是先左移一位，然后去S盒中进行替换操作，再进行异或

示例

将刚刚state化的密钥拿来
		31 35 38 34
		32 36 37 33
		33 37 36 32
		34 38 35 31	
分别为： W0 W1 W2 W3

先要获取W4，取出W3
34			33				c3 					（01）
33 变为->	   32 进行S盒变换-> 23 和Wi-4异或再和Rcon （00）异或得到 W4
32			31				c7					（00）
31			34				18					（00）

if (i%4 != 0)
Wi = Wi-1 ^ Wi-4

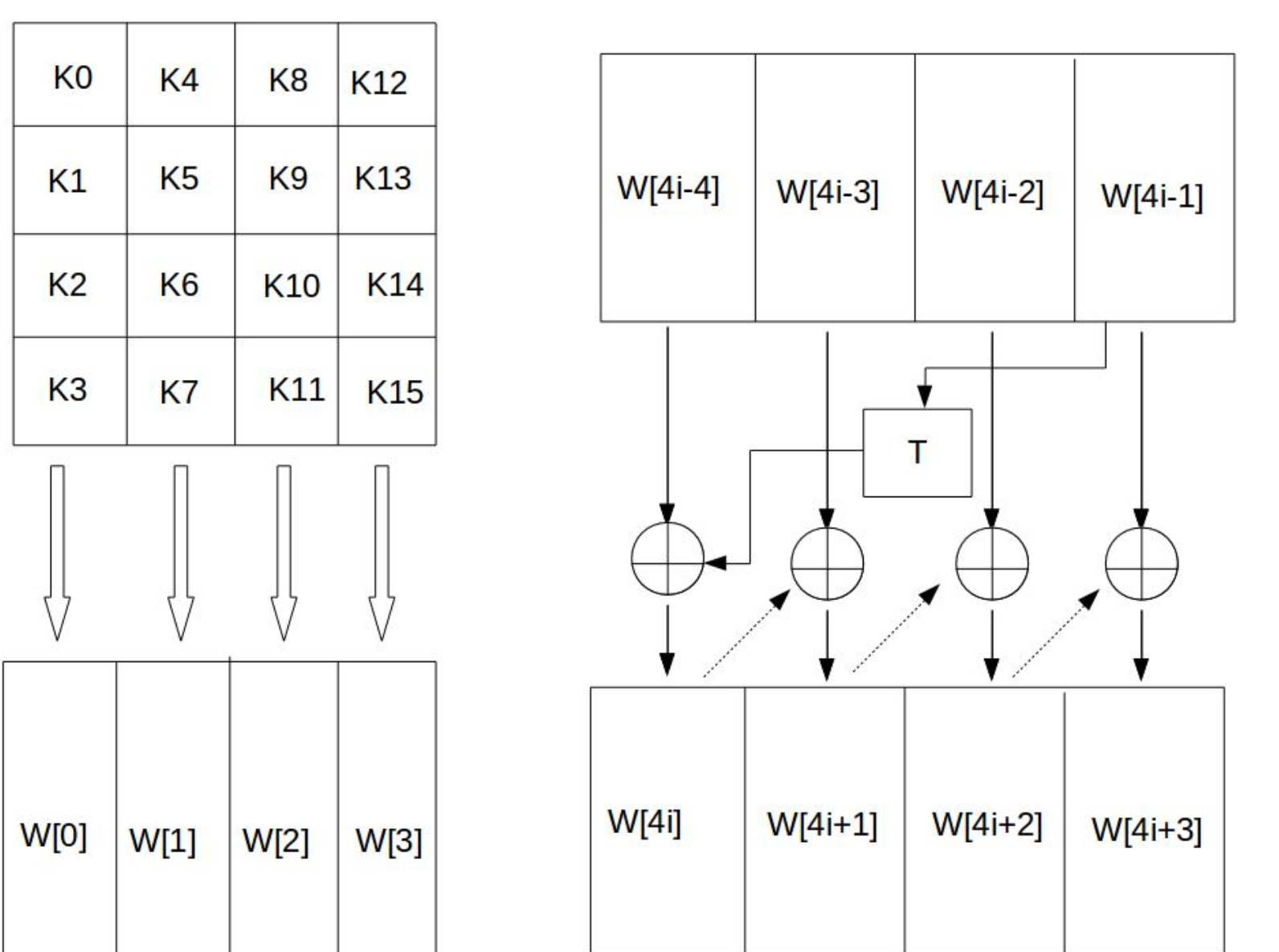
一共生成 4-43 四十个子密钥加上种子密钥一共 44 个，总共使用十一轮，一轮使用四种，种子密钥在开始轮换之前 AddRoundKey 异或的就是种子密钥。这样的子密钥是算出来的，还有一种查表法，直接查，加密速度更快。只是内存较计算的占用多

查表法

查表法进行的操作就是将S盒替换、循环左移和列混合融合成一步。跳过计算过程，直接去取值，运算速度加快

https://zhuanlan.zhihu.com/p/42264499

查表法对内存配置有一定要求，目前是没啥大事了，好多软件中的AES已经使用了查表法，运算速度快